リスク比の信頼区間
ポイント:比の対数をとり、正規近似する
リスク比は疫学における指標の1つです.一般的には相対危険度(相対リスク,relative risk,RR)として利用されています.
xm <- matrix(c("a","b","c","d"), nrow=2, byrow=T) name <- list("暴露"=c("あり(A群)","なし(B群)"),"疾病"=c("あり","なし")) dimnames(xm)<-name xm 疾病 暴露 あり なし あり(A群) "a" "b" なし(B群) "c" "d"
前提
比は分母が小さくなると、数値が大きくなりすぎて正規近似の精度が悪くなります.比の対数であれば高い精度で正規近似することが可能になります. したがって、比の対数を考えていくことになります.
定義と言葉の整理
標本比率 の母比率を
標本比率 の母比率を
,
リスク差(過剰絶対リスク) =
リスク比 RR = A群のB群における疾病の頻度の比
過剰リスク(過剰相対リスク) =
オッズ比=
リスク比の信頼区間
比の対数を考えていきます.
標本のリスク比=標本リスク比( =
)、母集団のリスク比を母リスク比(
=
)とします.
標本リスク比の対数
、 母リスク比
の対数
正規近似で信頼区間を求めていくためには、以下の式が必要になります.
したがって、以下の式が95%信頼区間を求める式になります
以下、 とします
より
デルタ法(delta method)によって近似的に求めたもの
「矢野様より指摘いただき、修正しております」
#Rで95%信頼区間を求めてみます rr <- a*(c+d)/(a+b)/c # = (a/(a+b))/(c/(c+d)) exp(log(rr)+qnorm ( c(0.025,0.975) )*sqrt(b/a/(a+b)+d/c/(c+d))) または exp(log(rr)+c(-1,1)*qnorm (0.975)*sqrt(b/a/(a+b)+d/c/(c+d))) 例) クロス表イメージ matrix(c(76, 399, 129, 332),2,byrow=T) [,1] [,2] [1,] 76 399 [2,] 129 332 a<-76; b<-399; c<-129; d<-332 #参考web2より ( rr <- a*(c+d)/(a+b)/c ) #リスク比 [1] 0.5717829 rr*exp(qnorm ( c(0.025,0.975) )*sqrt(b/a/(a+b)+d/c/(c+d))) [1] 0.4440632 0.7362370 または rr*exp(c(-1,1)*qnorm (0.975)*sqrt(b/a/(a+b)+d/c/(c+d))) [1] 0.4440632 0.7362370
参考web1 R -- 相対危険度(対応のない場合)
参考web2 R による統計処理
参考文献)柳川 堯 ; 観察データの多変量解析―疫学データの因果分析,近代科学社 ,2016
有意差とは・・・?
乱数を発生させて、set.seed( )で記憶させてシミュレーションしてみます
乱数なので再現できませんが、set.seed( )を使用することで再確認できます
set.seed(1) #もう一度確かめたいときはset.seed( )で乱数を記憶させておきます.( )の中は何でもOK. x20 <- rnorm(20,3.25,2.25) #平均3.25,標準偏差2.25のデータ(乱数)20個 set.seed(2) y20 <- rnorm(20,2.12,1.95) #平均2.12,標準偏差1.95のデータ(乱数)20個 t.test(x20,y20) #独立した2群の差の検定を実施してみます Welch Two Sample t-test data: x20 and y20 t = 1.808, df = 37.999, p-value = 0.07852 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.1409049 2.4959643 sample estimates: mean of x mean of y 3.678679 2.501149 ♯ p-value = 0.07852 危険率0.05でも有意差は認められませんでした・・・
次に同じ平均値、同じ標準偏差で100個ずつ用意して、検定してみます
set.seed(3) x100 <- rnorm(100,3.25,2.25) set.seed(4) y100 <- rnorm(100,2.12,1.95) t.test(x100,y100) Welch Two Sample t-test data: x100 and y100 t = 3.6836, df = 196.81, p-value = 0.0002971 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0.4491119 1.4841008 sample estimates: mean of x mean of y 3.274830 2.308224 P = 0.0002971 危険率0.01でも有意差あり!
統計量(この場合はt値)を考えれば当然の結果なのですが、
まだこのことに気づかずに有意差のみで議論している理学療法士も多いようです.
独立した2群であれば、それぞれのサンプルを増やすことで有意差を出すことが可能になります!
では、箱ひげ図で確認してみます
boxplot(x20,y20,x100,y100,xaxt="n") name<-c("x20","y20","x100","y100") axis(side=1,at=c(1,2,3,4),labels=name)

x20とy20に有意差がなくて、x100とy100に有意差がある・・・ようには見えませんね!
平均値と標準偏差が等しい正規分布からの乱数ですので、同じような箱ひげ図になるのは当然です.
x20とy20に有意差がなくて、x100とy100に有意差があるという結果の理解に苦しみます.
ここに数字のマジックが隠れています.
どのように有意差検定を実施しているのか、理解することが必要になります.
以下のページで、n増加→統計量大→p値小の構図が理解できると思います.
さて次はどうでしょうか?
# x20,y20の平均値は同じで、標準偏差を1/10にしてみましょう set.seed(5) x202 <- rnorm(20,3.25,0.225) set.seed(6) y202 <- rnorm(20,2.12,0.195) t.test(x202,y202) Welch Two Sample t-test data: x202 and y202 t = 15.657, df = 37.994, p-value < 2.2e-16 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0.8960426 1.1621642 sample estimates: mean of x mean of y 3.186874 2.157771 # p-value = 2.2e-16 危険率0.01でも有意差あり!
箱ひげ図で確認してみましょう.
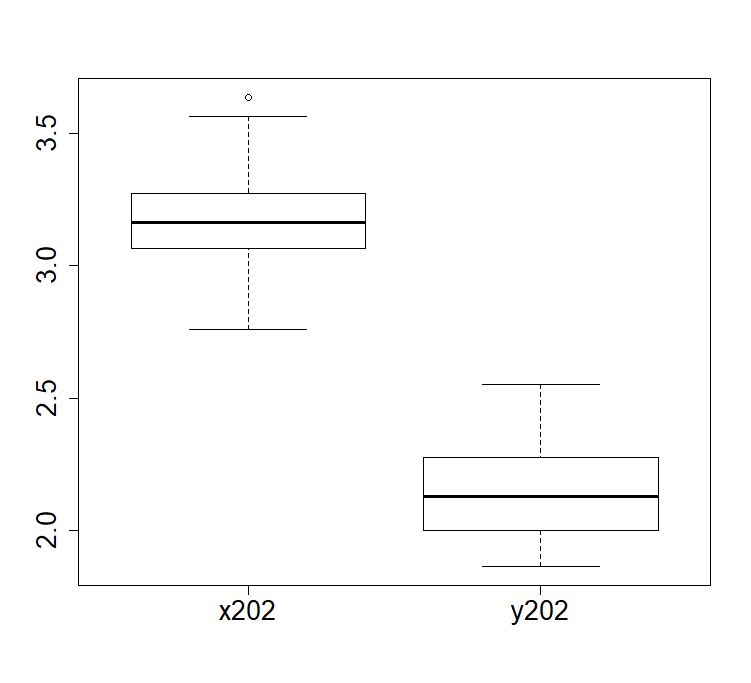
平均値が同じでも、ばらつき(分散、標準偏差)に違いがあれば統計結果は異なります.
有意差に一喜一憂するのではなく、サンプル数や分散、またそのデータがもつ性質をよく考えて、差を考察するべきです.P値よりも信頼区間や効果量などが比較の参考になるでしょう.
yoshida931.hatenablog.com
平均
算術平均 arithmetin mean (=相加平均)
1回 10人 2回 15人 3回 8人 平均回数は (10*1+15*2+3*8)/(10+15+8)
度数分布からの平均
真の平均の近似値なので多少のズレが生じます
最初と最後の階級が少ない場合には無視して求めます(年収平均など)
無視できない数であれば、最初の下限は0にして、最後の上限は直線の範囲と同じ範囲にします
幾何平均 geometoric mean (=相乗平均)
そもそも「幾何」とは、「いくばく」と読むので、わずか・すこしという意味があります 例1)利回りの例で考えてみます
10%, 15%, -5%, 13% と年々変化する利回り 平均は ( 1.1 + 1.15 + 0.95 + 1.13 ) / 4 =1.0825 ではありません! 正解は・・・ ( 1.1 * 1.15 * 0.95 * 1.13 )^(1/4) = sqrt( sqrt( 1.1 * 1.15 * 0.95 * 1.13 ) ) =1.079501 年平均利率は7.95%が正解です 奇数の場合は対数で計算します
例2)極端な例ですが、消費税で考えます
100円の品物の買う場合に 昨年5%になり、翌年15%に引きあがりました この2年間の平均上昇率は何%でしょうか? ( 5 + 15 ) / 2 = 10% ではありません (1.05 * 1.15 ) ^ (1/2) =1.098863 平均9.88%が正解です
調和平均 harmonic mean
距離÷時間=速度を例にとって考えてみます
片道100kmを往復します 往路は10km/h, 復路は15km/hかかりました 平均速度は(10+15)/2=12.5km/hではありません 往路の時間は100/10時間、復路の時間は100/15時間で合計50/3時間になります したがって平均時速は (100*2)/( (100/10)+(100/15) ) = 12 km/h
データフレームからの抽出
例)ChickWeightからDietの1と3だけ抜き出す
subset(ChickWeight,subset = Diet==c(1,3))
例)iris アヤメ
head(iris,5) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa
Sepal.Length(へたの長さ)とSpecies(種)
2列のみを抽出したフレームにします
irisSL <- subset(iris,select = c(Sepal.Length, Species)) head(irisPW,5) Sepal.Length Species 1 5.1 setosa 2 4.9 setosa 3 4.7 setosa 4 4.6 setosa 5 5.0 setosa
つぎに列を種(3種類)にしてへたの長さを提示します
iun2 <- unstack(irisSL,formula = Petal.Width ~ Species) head(iun2,10) setosa versicolor virginica 1 5.1 7.0 6.3 2 4.9 6.4 5.8 3 4.7 6.9 7.1 4 4.6 5.5 6.3 5 5.0 6.5 6.5
Sepal.Length(へたの長さ)とSpecies(種)の2列に戻します
x<-c(iun2$setosa,iun2$versicolor,iun2$virginica) Species <- c(rep("setosa",50),rep("versicolor",50),rep("virginica",50)) xy <- data.frame(Sepal.Length=x, Species) Sepal.Length Species 1 5.1 setosa 2 4.9 setosa 3 4.7 setosa 4 4.6 setosa 5 5.0 setosa 6 5.4 setosa
irisのvirginicaだけを抜き出す方法
ise <- split(iris,iris[5]) #irisの5列目の項目で分割 head(ise$virginica) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 101 6.3 3.3 6.0 2.5 virginica 102 5.8 2.7 5.1 1.9 virginica 103 7.1 3.0 5.9 2.1 virginica 104 6.3 2.9 5.6 1.8 virginica 105 6.5 3.0 5.8 2.2 virginica 106 7.6 3.0 6.6 2.1 virginica
Sepal.Lengthの順に並べ換えます
Sepal.Lengthの昇順に並び替え ise <- split(iris,iris[5]) #irisの5列目の項目で分割 isev <- ise$virginica isevo <- isev[order(isev$Sepal.Length),] head(isevo) Sepal.Length Sepal.Width Petal.Length Petal.Width Species 107 4.9 2.5 4.5 1.7 virginica 122 5.6 2.8 4.9 2.0 virginica 114 5.7 2.5 5.0 2.0 virginica 102 5.8 2.7 5.1 1.9 virginica 115 5.8 2.8 5.1 2.4 virginica 143 5.8 2.7 5.1 1.9 virginica ````
ベイズの定理
ベイズの定理とは「観測値(データ)で条件付けられた、母数の分布を与える定理 」です
#Rのサンプル women$height を使用します x <- women$height #標本平均 me <- mean(women$height) =65 #標本標準偏差 sd <- sqrt(sum((x - mean(x))^2) / length(x)) =4.32
女性の伸長(インチ)の平均65、標準偏差4.32を正規分布の母数と見立ててしまえば、95%予測区間を導き出すことは簡単です.
しかし、x~N(65,4.3)の分布が真の分布とは言えません.x~N(64,4.5)やx~N(66,4.6)などの母分散も考えられます.つまり、母数(平均や標準偏差)も分布することが考えられます.
確率密度関数 f(母数|観測値) の分布
例として母数を平均値, 標準偏差とします
平均値, 標準偏差 とデータxは独立していないので条件付き分布となります
条件付き分布
f (x,θ) ≠ f(x)*f(θ) # x が与えられた場合 f (x,θ) = f(x)*f (θ|x) # θ が与えられた場合 f (x,θ) = f (x|θ)*f(θ)
分布に関するベイズの定理
観測値(データ)で条件付けられた、母数の分布を与える定理
f (x,θ) = f(x)*f (θ|x)より f (θ|x) = f (x,θ) ÷ f(x) = f (x|θ)*f(θ) ÷ f(x)
上記式より
確率に関するベイズの定理
Aを得られた結果とします.Bをその原因とします.
例)5つの袋に赤白の玉が入り混ざっています.どれかの袋から玉が取られたとします.
取り出した玉=結果A
どの袋から取り出したか=原因B
結果Aが得られた原因Bを推定します.袋が5つなのでB1, B2, B3, B4, B5 が原因となります. ベイズの定理では、結果Aであったときに原因が、B1またはB2またはB3またはB4またはB5 である確率を算出することになります.
ベイズの定理
証明
A = A∩Ω
=A∩(B1∪B2∪…∪Bi)
=(A∩B1)∪(A∩B2)∪...∪(A∩B1)
∴
例)ベイズの逆確率
袋B1または袋B2から一つの球を取り出します.
B1には白玉3個、赤玉2個
B2には白玉1個、赤玉3個
取り出した球が赤だった場合(事象A)、袋がB1である確率、B2である確率を求めよ.
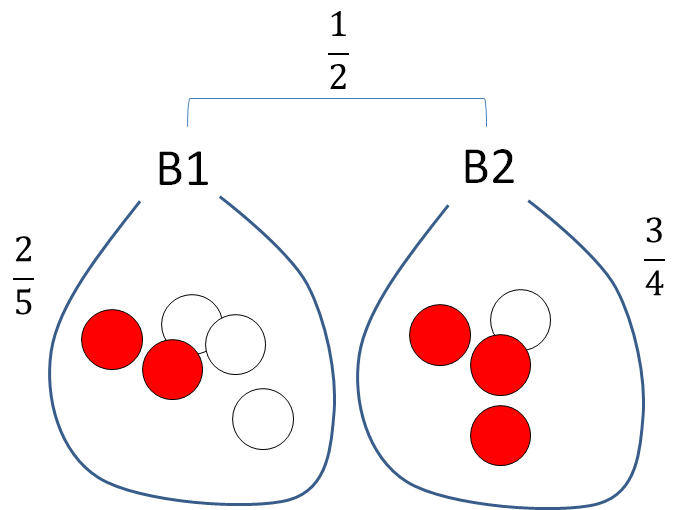
正規化

# 赤玉を引いた袋がB1である確率(ベイズの逆確率) P(B1|A)= (1/2)*(2/5) / ((1/2)*(2/5) + (1/2)*(3/4)) = 0.3478261 # 赤玉を引いた袋がB2である確率(ベイズの逆確率) P(B2|A)= (1/2)*(3/4) / ((1/2)*(2/5) + (1/2)*(3/4)) = 0.6521739 #正規化しているので P(B1|A) + P(B2|A) = 1



