ベイズの定理
ベイズの定理とは「観測値(データ)で条件付けられた、母数の分布を与える定理 」です
#Rのサンプル women$height を使用します x <- women$height #標本平均 me <- mean(women$height) =65 #標本標準偏差 sd <- sqrt(sum((x - mean(x))^2) / length(x)) =4.32
女性の伸長(インチ)の平均65、標準偏差4.32を正規分布の母数と見立ててしまえば、95%予測区間を導き出すことは簡単です.
しかし、x~N(65,4.3)の分布が真の分布とは言えません.x~N(64,4.5)やx~N(66,4.6)などの母分散も考えられます.つまり、母数(平均や標準偏差)も分布することが考えられます.
確率密度関数 f(母数|観測値) の分布
例として母数を平均値, 標準偏差とします
平均値, 標準偏差 とデータxは独立していないので条件付き分布となります
条件付き分布
f (x,θ) ≠ f(x)*f(θ) # x が与えられた場合 f (x,θ) = f(x)*f (θ|x) # θ が与えられた場合 f (x,θ) = f (x|θ)*f(θ)
分布に関するベイズの定理
観測値(データ)で条件付けられた、母数の分布を与える定理
f (x,θ) = f(x)*f (θ|x)より f (θ|x) = f (x,θ) ÷ f(x) = f (x|θ)*f(θ) ÷ f(x)
上記式より
確率に関するベイズの定理
Aを得られた結果とします.Bをその原因とします.
例)5つの袋に赤白の玉が入り混ざっています.どれかの袋から玉が取られたとします.
取り出した玉=結果A
どの袋から取り出したか=原因B
結果Aが得られた原因Bを推定します.袋が5つなのでB1, B2, B3, B4, B5 が原因となります. ベイズの定理では、結果Aであったときに原因が、B1またはB2またはB3またはB4またはB5 である確率を算出することになります.
ベイズの定理
証明
A = A∩Ω
=A∩(B1∪B2∪…∪Bi)
=(A∩B1)∪(A∩B2)∪...∪(A∩B1)
∴
例)ベイズの逆確率
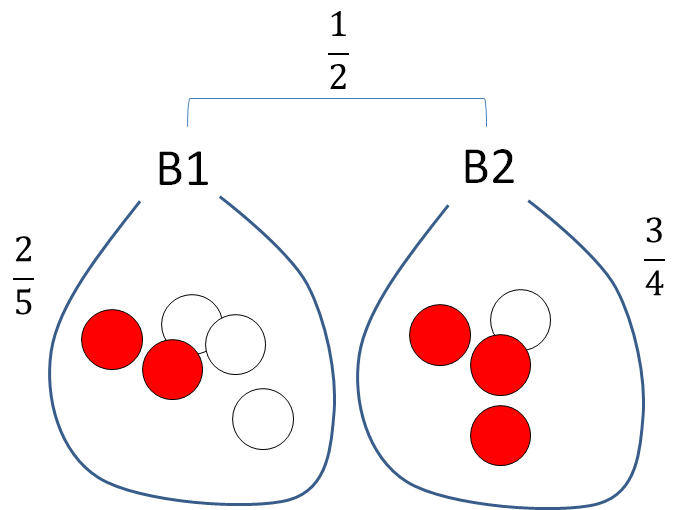
袋B1または袋B2から一つの球を取り出します.
B1には白玉3個、赤玉2個
B2には白玉1個、赤玉3個
取り出した球が赤だった場合(事象A)、袋がB1である確率、B2である確率を求めよ.
正規化

# 赤玉を引いた袋がB1である確率(ベイズの逆確率) P(B1|A)= (1/2)*(2/5) / ((1/2)*(2/5) + (1/2)*(3/4)) = 0.3478261 # 赤玉を引いた袋がB2である確率(ベイズの逆確率) P(B2|A)= (1/2)*(3/4) / ((1/2)*(2/5) + (1/2)*(3/4)) = 0.6521739 #正規化しているので P(B1|A) + P(B2|A) = 1