2標本 平均の差の検定
下記のサイトに移転しました
確率点と累積分布
確率点と累積分布
投稿日2017.7.22
更新日2017.9.1
lower.tailのdefaultはTRUE
この意味が重要です.勉強のためにdefaultのTRUEも挿入しときます.
lower.tail
logical; if TRUE (default), probabilities are P[X ≤ x] otherwise, P[X > x].
Rのhelpより
#上側確率が0.025になるZ値 qnorm(0.975, lower.tail = TRUE) = 1.959964 # Z=1.959964 より下側の累積確率が0.975 ) qnorm(0.975, lower.tail = FALSE) = -1.959964 # Z= -1.959964 より上側の累積確率が0.975 ) #上側確率が0.025になる累積分布 pnorm(1.96, lower.tail = TRUE) = 0.9750021 #下側確率が0.025になる累積分布 pnorm(1.96, lower.tail = FALSE) = 0.0249979
二項分布
イメージするためにグラフ挿入 x <- 0:3 y <- c(dbinom(x, 3, 0.5)) names(y) <- x barplot(y)

#試行回数n, 成功回数x, 確率pの場合の累積確率は dbinom(n, x, p) #確率0.5のベルヌーイ試行(成功,失敗)で3回実施して成功が2回以内の確率は pbinom(2, 3, 0.5, lower.tail = TRUE) = 0.875 #確率0.5のベルヌーイ試行(成功,失敗)で3回実施して成功が2回以上の確率は pbinom(2, 3, 0.5, lower.tail = FALSE) = 0.125
t分布
#自由度10、上側確率が0.025になるt値 qt(0.975, 10, lower.tail = TRUE) = 2.228139 #下側確率が0.025になるt値 qt(0.025, 10, lower.tail = TRUE) = qt(0.975, 10, lower.tail = FALSE) = -2.228139
F分布
#自由度(6, 24), 確率0.05のF値 qf(0.95, 6, 24, lower.tail = TRUE) = 2.508189 #自由度(6, 24), F値がfの場合の累積確率 pf(f, 6, 24, lower.tail = TRUE) = 0.95 #その場合のp値 pf(f, 6, 24, lower.tail = FALSE) = 1 - pf(f, 6, 24) = 0.05
ブログの再構成
自分が書いたブログなのに「見にくい&理解できない」 という悩みが募ってきました. よって、少しずつ再構成することにしました. はてな記法なるものに初挑戦! 見直したとき、せめて・・・ せめて書いた本人が理解できるような内容に改めたいと思っております.
モンティ・ホール問題
モンティ・ホール問題
投稿日2017.8.30
モンティ・ホール問題、モンティ・ホール・ジレンマ
Rを使って何とか解いてみようと思います.
3つのドアのうち1つのドアの後ろには高級車(車の扉)があり、残りの2つのドアにはヤギ(ヤギの扉)がいます。司会者は、どのドアの後ろに高級車があるのかを知っています。
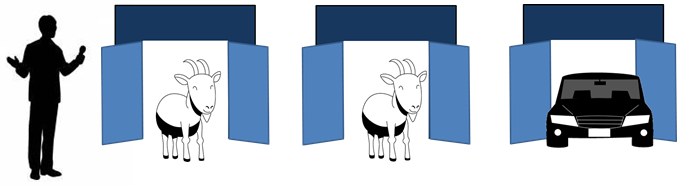
あなたが1つのドアを選んだ(最初の扉)あと、司会者はあなたが選んでいない2つのドアの1つのドアを開けてヤギがいることを教えてくれます。
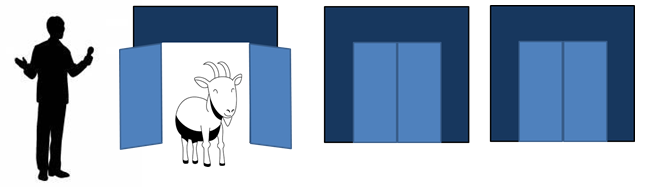
そして司会者は・・・
「はじめに選んだドア(最初の扉)のままでもよいし、いま閉じられているドアを選択してもよい」と言ってきました。司会者はウソはつきません。あなたははじめに選択したドアのままにしますか?それともドアを変更しますか?
出典:稲葉由之 ;プレステップ統計学II 推測統計学,弘文堂,2013,p30
残り二つの扉、どちらを選択しても確率は1/2のように思えるのですが・・・
嘘みたいですけど、このことが長年大論争になったそうです.今回は、Rを使って確率の勉強をしてみたいと思います.

このように考えると、扉を変更した方が2/3になりそうだけど・・・1/2じゃない
10回、100回、1000回・・・やったらどうなるかいな?
ということでRを使ってシミュレーションを実行してみます
まず扉のNoを1,2,3とします

扉には doors <- c(1:3) という名前をつけます.
車の扉、最初の扉、ヤギの扉をランダムに割り当ててみます.
もちろん車の扉=最初の扉の場合もありますので、「車の扉」と「最初の扉」の抽出は復元抽出になります.
sampleを使用してランダム抽出します
car <- sample(doors, 1) you <- sample(doors, 1)
扉を変えない場合
notcha <- function(x){ doors <- c(1:3) x <- 0 car <- sample(doors, 1) #ランダム抽出で車の扉を設定 you <- sample(doors, 1) #ランダム抽出で最初の扉を設定 if(car == you){ #もし最初の扉に車の扉だったら1点加える x <- x + 1 } return(x) } notcha() y <- 0 for(i in 1:10000) { # fro(i in 1:n){} ・・・{}をn回繰り返す y <- y + notcha() } y
10000回実施したら3302回でした.約1/3です.
扉を変えた場合
chan <- function(x){ x <- 0 doors <- c(1:3) car <- sample(doors, 1) #ランダム抽出で車の扉を設定 you <- sample(doors, 1) #ランダム抽出で最初の扉を設定 if(you == car){ x <- x + 0 #最初に選んだ扉に車がある場合、0点となります }else{ x <- x + 1 #最初の扉に車がない場合、残るヤギの扉は司会者が明けているので、必ず車の扉を選択することになります } return(x) } chan() y <- 0 for(i in 1:10000) { # fro(i in 1:n) {} ・・・{}をn回繰り返す y <- y + chan() } y
10000回実施した確率は6656回でした.約2/3です.
こんな解き方では異論が多いと思いますので、スマートな方法をネットで検索してみてください

モンテカルロ法で円周率を求める
モンテカルロ法で円周率を求める
投稿日2017.8.28
対象となるある現象がいくつかの確率変数の関数で表現できる場合(数値モデル)、各変数で仮定される確率分布に沿った標本値を大量に生成(乱数)して、その計算結果の分布を推定(結果の推定)する方法です。
数値モデル → 乱数挿入 → 結果の推定
モンテカルロ法を使用して円周率 (π) を求めてみます

上図の四角の中にランダムに点を打ってみます

四角の面積は 2×2=4、円の面積は π × 1^2 = π
打った点の個数をn、円の中に入った個数をmとします
非常に多くの点を打つことで四角の中は塗りつぶされます

そこで次のような比率を考えます
点を多く打つことで、全体の点の数と円内の点の数との比が
四角の面積と円の面積の比に等しくなるはずです.
n : m = 4 : π
π=4 × m / n (数値モデル)
Rを使用してnの乱数を多く作成すれば円周率が求められることになります
ではやってみます
一様乱数から(x,y)を作成します (乱数)
-1<x<1, -1<y<1
試しに5組分だけ作成してみます
dat<-matrix(runif(5*2,-1,1),2)

イメージ
一行目をx、二行目をyとして x^2 + y^2 < 1 となる点の個数が
円内の個数mということになります
m<-colSums(dat^2) < 1
全ての点をプロットしてmは赤で示します
plot( dat [1,], dat [2,], col = (2-m) , pch = 20 )
m はcolSums(dat^2) < 1の場合にはTRUE=1、それいがいはFALSE=0 ここがポイント
col=(2-m)とした場合には円内に入ったら1(黒)、円外では2(赤)となります
これまでの式をまとめて100個打ってみます
dat<-matrix(runif(100*2,-1,1),2)
m<-colSums(dat^2) < 1
plot( dat [1,], dat [2,], col = (2-m) , pch = 20 )

分かりにくいので10000個打ってみます
dat<-matrix(runif(10000*2,-1,1),2)
m<-colSums(dat^2) < 1
plot( dat [1,], dat [2,], col = (2-m) , pch = 20 )

おっ!円が見えてきました!!!
ちょっと感動
dat<-matrix(runif(n*2,-1,1),2)
m<-colSums(dat^2) < 1
plot( dat [1,], dat [2,], col = (2-m) , pch = 20 )
結果の推定
π=4 × m / n を推定します
上記の結果より
π=4 × m / 10000 = 3.1388 (乱数なので結果は異なります)
まとめて関数にしてみます
pai<-function(n){
dat<-matrix ( runif ( n*2 , -1 , 1 ) , 2 )
m<-colSums( dat^2 ) < 1
pl<-plot( dat [1,] , dat [2,] , col = (2-m) , pch = 20 , xlab = n , ylab = "" )
return( ( 4*sum( m ) ) / n )
}
nを100,500,1000,5000と変更して図を描いてみます
par(mfrow = c(2,2))
pai(100) ;pai(500) ;pai(1000) ;pai(5000)
dev.off()


n=100 π= 3.4
n=500 π= 3.128
n=1000 π= 3.144
n=5000 π= 3.1352