二元配置分散分析(各水準の信頼区間推定)
二元配置分散分析(各水準の信頼区間推定)
投稿日2017.8.24
各要因における各水準の母平均の区間推定

繰り返し数 n

n = 繰り返し数
要因1水準Aの有意水準αの信頼区間は、xai ± t α/2 (自由度) * 標準誤差 となります. 母分散が未知なので、標準誤差を残差の平均平方(不偏分散) / 水準のサイズ としてます.したがってtの自由度は、残差の平均平方 の自由度になります.
95%信頼区間
xai ± t 0.025 ( f*g*(n-1) ) * 標準誤差
例)次の水準Aの95%信頼区間を求めてみます


xai
= mean(c(s1,s2,s3))
= 13.1333
自由度2*3*(5-1)=24, 有意水準5%のt値は t(24)(0.025)
qt ( 0.975 ,24 ,lower.tail=TRUE )
= 2.063899
残差の平均平方(不偏分散)は3.08
残差の標準誤差は√(3.08/5*3) = √(3.08/15)
したがってxa1.の95%信頼区間は
mean ( c (s1,s2,s3) ) - 2.063899 * sqrt ( 3.08/15 )
= 12.1981
mean ( c (s1,s2,s3) ) + 2.063899 * sqrt ( 3.08/15 )
= 14.06856
次のような式で表現できます

交互作用がない場合
Ai水準での母平均の推定量は xai.
Ai水準での95%信頼区間は xai. ± t 0.025 ( de(e) ) × √ ( V(e) / g×n )
Bi水準での母平均の推定量は xa.j
Ai水準での95%信頼区間は xa.j ± t 0.025 ( de(e) ) × √ ( V(e) / f×n )
交互作用がある場合
(AiBj) での母平均の推定量は xaij
(AiBj) での95%信頼区間は xaij ± t 0.025 ( de(e) ) × √ ( V(e) / n )
トービット回帰直線
トービット回帰直線
投稿日2017.8.4
打ち切りデータの場合、つまり天井効果や床効果が生じているデータの場合には、トービット回帰直線で分析します.
参考書はもちろん
豊田秀樹 (著, 編集);回帰分析入門 (Rで学ぶ最新データ解析) ,東京図書 ,2012
Rのサンプルanscombeを使います.( n=11の4セット )
x1<-anscombe$x1
x4<-anscombe$x4
y1<-anscombe$y1
y4<-anscombe$y4
par(mfrow = c(1,2))
plot(x1,y1,xlab = "図A",ylab = "")
plot(x4,y4,xlab = "図B",ylab = "")

dev.off()
図A 通常の散布図
lm1<-lm(y1~ x1,data= anscombe)
plot(x1,y1)
abline(lm1$coefficients[1],lm1$coefficients[2])

視覚的にも何となくこの直線でフィットしているように見えます
x軸を予測値にして、残差を標準化して更に見やすくしてみます
ei<- y1-( lm1$coefficients[1]+ lm1$coefficients[2]* x1)
eis<-ei/sqrt( (sum(ei^2) )/(11 - 2) ) #標準化残差
plot(lm1$coefficients[1]+ lm1$coefficients[2]* x1, eis,xlab="図A(x軸:予測値)",ylab=" ", xaxt="n")
abline(h=0, lty=2, col=2)

図B 打ち切りデータがある場合
トービット回帰直線( 関数vglmを使用 )
通常の回帰直線(実践)
y4x4 <- lm(y4 ~ x4); summary(y4x4)
plot(x4,y4)
abline(summary(y4x4)$coefficients1,summary(y4x4)$coefficients2)
関数vglmを使用してトービット回帰直線を破線で加えます
y4x4t <- vglm(y4 ~ x4, tobit(Lower=8, Upper=19), trace=TRUE); summary(y4x4t)
abline(summary(y4x4t)@coefficients1,summary(y4x4t)@coefficients3,lty=2)

床効果で下に引っ張られていた回帰直線をやや上方修正できました.
ユールのQ
ユール ( Yule ) のQ
ユールの関連係数、ユールの連関係数とも呼ばれています.関連が強いほど1または-1に近い値をとります。

Q= ( a*d - b*c ) / ( a*d + b*c ) = ( オッズ比 - 1 ) / ( オッズ比 + 1 )
例)2つの質問 ( q1 , q2 ) に関する答え ( yes , no ) のベクトルを考えます.
q1<-c("yes","yes","yes","yes","yes","yes","yes","no","no","no")
q2<-c("yes","yes","yes","no","no","no","no","yes","yes","no")
tq<- table ( q1,q2 )
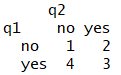
Q = ( 1*3 - 2*4 ) / ( 1*3 + 2*4 )
= - 0.4545455
Rの関数で確認してみます
install.packages("psych")
library(psych)
Yule(tq)
= - 0.4545455