ユールのQ

ユール ( Yule ) のQ
ユールの関連係数、ユールの連関係数とも呼ばれています．関連が強いほど1または-1に近い値をとります。

Q= ( a*d - b*c ) / ( a*d + b*c ) =  ( オッズ比 - 1 ) / ( オッズ比 + 1 )

例）2つの質問 ( q1 , q2 ) に関する答え ( yes , no ) のベクトルを考えます．
q1<-c("yes","yes","yes","yes","yes","yes","yes","no","no","no")
q2<-c("yes","yes","yes","no","no","no","no","yes","yes","no")

tq<- table ( q1,q2 )　   

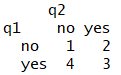
Q = ( 1*3 - 2*4 ) / ( 1*3 + 2*4 )
    = - 0.4545455

Rの関数で確認してみます
install.packages("psych")
library(psych)
Yule(tq)
= - 0.4545455

適合度の検定 (ピアソンの 𝜒^2 適合度検定)

下記のサイトに移転しました

y2pt.com

Rstudioでの data.frame 表示の不具合

データフレームを表示したときに、ラベルが見えなくなりました

RStudio-1.0.143 から RStudio-1.0.153 へバージョンアップすることで不具合は解消しました．
https://www.rstudio.com/products/rstudio/download/preview/

Rstudioのサポートページの掲示板で助言を受けました！

https://www.rstudio.com/

ファイ係数

連関係数
　クロス集計表における2つの変数間の関連性の程度を表す指標として，連関係数が提案されています．

連関係数＜｜0.2｜　連関はほとんどない
｜0.2｜≦連関係数＜｜0.4｜　やや連関がある
｜0.4｜≦連関係数＜｜0.7｜　強い連関がある
｜0.7｜≦連関係数　かなり強い連関がある
　　　対馬栄輝; よくわかる医療統計 -「なぜ?」にこたえる道しるべ, 東京図書, 2015

ファイ係数 (φ係数)
　クロス集計表における行要素と列要素の関連の強さを示す指標. 1と0の2つの値からなる変数に対して計算される相関係数です。つまり、２つの２値変数をそれぞれ1と0で数値化した上で算出した積率相関係数です。1と0の2つの値とは、「好き、嫌い」、「はい、いいえ」など、2択で表現されるデータです. 選択肢Aに0を、選択肢Bに1を割り付けることで、ファイ係数を求めることができます.

例）2つの質問 ( q1 , q2 ) に関する答え ( yes , no ) のベクトルを考えます．
q1<-c("yes","yes","yes","yes","yes","yes","yes","no","no","no")
q2<-c("yes","yes","yes","no","no","no","no","yes","yes","no")
q101<-ifelse(q1=="yes",1,0)        # 0,1のベクトルに変更
  q101 <- c(1, 1, 1, 1, 1, 1, 1, 0, 0, 0)
q201<-ifelse(q2=="yes",1,0)       # 0,1のベクトルに変更
  q201 <- c(1, 1, 1, 0, 0, 0, 0, 1, 1, 0)

ピアソンの積率相関係数を2行×2列のクロス集計表に適用したもの
　　　ピアソンの積率相関係数

           

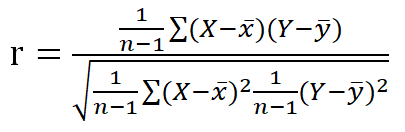
mean ( q101 )
=0.7
mean ( q201 )
=0.5
sum ( ( q101-0.7 ) * ( q201 - 0.5 ) )
= - 0.5
sum ( ( q101 - 0.7 )^2 )
=2.1
sum ( ( q201 - 0.5 )^2 )
=2.5
r = - 0.5 / sqrt ( 2.1 * 2.5 )
  = - 0.2182179

Rの関数で確認してみます
cor(q101,q201)                #相関係数をcor( )で算出
= - 0.2182179

次に例題をテーブルにして眺めてみます
tq<- table ( q1,q2 )　   

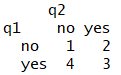
t<- tq [ c(2,1) , c(2,1) ] 　　
#これは不要ですがラベルの並べ替えです．yesから始めたいので挿入しておきます（1番目と2番目の入れ替え）

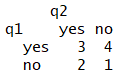
理解のためにデータフレームに変換します
t< - data.frame ( t )       

 
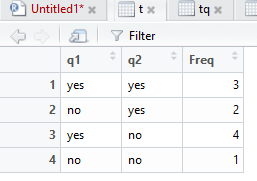
     q1   q2    Freq
1   yes  yes   3         #  t $ Freq[1]
2   no    yes   2        #  t $ Freq[2]
3   yes   no    4        #  t $ Freq[3]
4   no    no     1        #  t $ Freq[4]

ファイ係数φその1　ｶｲ二乗値より
φ＝√（ｶｲ二乗値/ｎ）
chisq.test ( tq , correct=F )
X-squared = 0.47619
φ＝sqrt ( 0.47619 / 10 )
= 0.2182178

ファイ係数φその2  観測値と周辺度数より

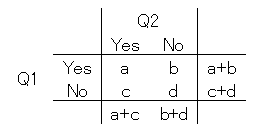
φ =  ( a*d - b*c ) / √ ( a+b )*( c+d )*( a+c )*( b+d )*
x <- t$Freq[1] * t$Freq[4] - t$Freq[2] * t$Freq[3]　  # x = 対角線上の観測値を掛けたものの差
y <- ( t$Freq[1] + t$Freq[3] )* 　                               # y = 全ての周辺度数を掛けたもの
  ( t$Freq[2] + t$Freq[4] )*
  ( t$Freq[1] + t$Freq[2] )*
  ( t$Freq[3] + t$Freq[4] )
φ ＝ x / sqrt(y)
    = - 0.2182179

Rの関数で確認してみます
install.packages ( "psych" )
library ( psych ) 
phi ( tq , digits=8 )
= - 0.2182179

イェーツの補正

イェーツの補正 / イェーツの連続修正（Yate's continuity correction）
　離散型分布を連続型分布に近似させて統計的検定を行う際に使用する修正です．2×2分割表のデータに対して行われ、より正確な検定が可能になります．「連続的なカイ二乗分布（自由度1のχ二乗分布）」に近似するために、2×2分割表の中で観察される「二項分布型度数の離散型の確率」を補正します．各々の観測値と期待度数の差の絶対値より0.5を差し引くことによりカイ二乗検定の式を調整します．計算の結果得られるカイ二乗値を減らすことになりp値が増加することになります．

例）
x<-c(116,244)
y<-c(76,44)
xy<-data.frame(x,y)

期待度数
sum(x) * sum(116+76) / sum(xy)
sum(y) * sum(116+76) / sum(xy)
sum(x) * sum(244+44) / sum(xy)
sum(y) * sum(244+44) / sum(xy)
xe<- c( sum(x) * sum(116+76) / sum(xy) , sum(x) * sum(244+44) / sum(xy) )
ye<- c( sum(y) * sum(116+76) / sum(xy) , sum(y) * sum(244+44) / sum(xy) )
xye<-data.frame(xe,ye)

ｶｲ二乗値
( 116 - xye[1,1] ) ^2 / xye [1,1] +
　( 76 - xye [1,2] ) ^2 / xye [1,2] +
　( 244 - xye [2,1] ) ^2 / xye [2,1] +
　( 44 - xye [2,2] ) ^2 / xye [2,2]
 = 35.01157

イエーツの補正 を実施したｶｲ二乗値
 ( abs ( 116 - xye[1,1] ) - 1 / 2 ) ^2 / xye[1,1] +
 　( abs ( 76 - xye[1,2] ) - 1 / 2 ) ^2 / xye[1,2] +
 　( abs ( 244 - xye[2,1] ) - 1/2 ) ^2 / xye[2,1] +
 　( abs ( 44 - xye[2,2] ) - 1/2 ) ^2 / xye[2,2]
 = 35.01157

Rの関数で確認します
chisq.test(xy)

Pearson's Chi-squared test with Yates' continuity correction
data:  xy
X-squared = 35.012, df = 1, p-value = 3.278e-09

サンプルは日本統計学会 (編集); 日本統計学会公式認定　統計検定２級対応 統計学基礎, 東京図書, 2012,p156の例7

符号検定

符号検定 ( sign test )　一標本問題
n個のうちｘ個以下の符号が他の符号と異なる確率を求める検定です．正と負が同じ確率で出るときに、正（または負）の値の数がxとなる確率が B ( n , 0.5 ) の2項分布に従うことを利用します．
例
y<- c (1.5, 1.1, 1.2, -1.2, 2.3)

yの中に含まれる負の値をもつ数は1個です．少なくとも4個は正になる確率を求めます． 5個中1個負になるか、または5個中全てが正になる確率 です．また例題では一つが負なのですが、一つが正になる場合も同じ確率になりるので両側確率を求めることになります．以下のグラフを見てみましょう．

x <- 0 : 5　                              #ｘ軸は成功回数
y <- dbinom ( x, 5, 0.5 )　    #ｙ軸は確率密度
plot ( x, y, type = "h", col = c(2, 2, 1, 1, 2, 2), lwd = 3 )
求める確率は以下の赤部分の合計

5個が全て正になる場合は  ₅C₀ = choose( 5 , 0 ) = 1
5個が全て正になる確率は　( 1/2 )^5 = 1/32
5個中1個が負になる場合は  ₅C₁ = choose( 5, 1 ) = 5 通り
5個中1個が負になる確率は　( 1/32 ) *5 = 5/32
5個中2個が負になる場合は  ₅C₂ = choose( 5, 2 ) = 10 通り
5個中2個が負になる確率は　( 1/32 ) *10 = 10/32

上記のように考えてｐ値を算出します．
yは5個中1個が負の数になっています．したがって5個のうち1個以下の符号が他と異なる確率を求めることになります．つまり少なくとも4個が同じ符号である確率を求めます．

1個が正になる確率＋全てが負になる確率＝ 5/32 + 1/32
1個が負になる確率＋全てが正になる確率＝ 5/32 + 1/32
ｐ値 =  ( 5/32 + 1/32 ) * 2 =  0.375

Rの関数で確かめます

2*pbinom ( 1, 5, 0.5 )
=0.375

上式は以下のようになります

5個が全て正になる確率
= choose ( 5,0 ) * ( 0.5^0 ) * ( 0.5^5 )　　#成功回数0回
= dbinom ( 0, 5, 0.5 )
= 0.03125

5個中1個が負になる確率
= choose ( 5,1 ) * ( 0.5^1 ) * ( 0.5^4 )　　#成功回数1回
= dbinom ( 1 , 5 , 0.5 )
= 0.15625

両側確率なので×2
{ dbinom ( 0 , 5 , 0.5 ) +  dbinom  ( 1 , 5 , 0.5 )  } *2 
= 0.375

nが大きい場合
E[x] = np  ,  V[x] = np ( 1 – p ) より　
p = 1/2 を代入して正規近似にて検定を行います．

なぜｔ検定を繰り返してはいけないのか？

なぜｔ検定を繰り返してはいけないのか
投稿日2017.2.24
修正日2017.7.9

sample は「石村卓夫;分散分析のはなし,東京図書,1992,p137」

A<-c(12,14,16)
B<-c(13,15,17)
C<-c(15,17,19)
D<-c(17,19,21)

x<-c(rep("A",3),rep("B",3),rep("C",3),rep("D",3))
y<-c(A,B,C,D)
stripchart(y~x,vertical=T,pch=1,cex=2,cex.axis=1.5)

視覚的にはAD間、BD間には差があるように見えます

以下、重要な前提です
Aの母平均をμa
Bの母平均をμb
Cの母平均をμc
Dの母平均をμd　とします
「μa=μb=μc=μd」を検定する場合にｔ検定を繰り返してはいけないのです．

一元配置分散分析

oneway.test(y~x,var.equal = T)
#F = 3.6875, num df = 3, denom df = 8, p-value = 0.06214
#有意水準5％で差が「ない」という結果になりました

#全ての群の母分散は等しいと仮定してt検定を繰り返してみます
AB<- t.test ( A , B , paired=FALSE , var.equal=T , conf.level=0.95 )
AC<- t.test ( A , C , paired=FALSE , var.equal=T , conf.level=0.95 )
AD<- t.test ( A , D , paired=FALSE , var.equal=T , conf.level=0.95 )
BC<- t.test ( B , C , paired=FALSE , var.equal=T , conf.level=0.95 )
BD<- t.test ( B , D , paired=FALSE , var.equal=T , conf.level=0.95 )
CD<- t.test ( C , D , paired=FALSE , var.equal=T , conf.level=0.95 )

#それぞれの検定結果のP値のみを取り出してみます
str ( AB [ [3] ] ) ; str ( AC [ [3] ] ) ; str ( AD [ [3] ] ) ; str ( BC [ [3] ] ) ; str ( BD [ [3] ] ) ; str ( CD [ [3] ] )

AB 0.573
AC 0.14
AD 0.0376
BC 0.288
BD 0.0705
CD 0.288

やはりAD間には有意水準5％で「差がある」という結果になりました．しかし分散分析では差がないという結果でした．

分散分析の帰無仮説
有意水準0.5において「μa=μb=μc=μd」である．

ｔ検定の帰無仮説
有意水準0.5において「μa=μb」かつ「μa =μc」かつ「μa =μd」かつ「μb=μc」かつ「μb=μd」かつ「μc=μd」である．言いかえれば、有意水準0.5で「6組全てに差が見られない」となり、対立仮説は「少なくとも一組には差がある」となります．

　「μa=μb」かつ「μa =μc」かつ「μa =μd」かつ「μb=μc」かつ「μb=μd」かつ「μc=μd」となる確率は ( 1 - 0.05 ) ^6 です．したがって、有意水準0.5と設定した検定で少なくとも一組には差がある確率が 1 - ( 1 - 0.05 ) ^6 ＝ 0.2649081 となり、有意水準26.5％の検定となってしまいます．つまりαエラーの危険性が高くなるのです．このような矛盾を解消するための手法が多重比較です.

多重比較（Tukey）を行ってみます

TukeyHSD ( aov (y ~ x) , ordered = TRUE )
Tukey multiple comparisons of means
95% family-wise confidence level
factor levels have been ordered

Fit: aov(formula = y ~ x)

$x
　　  diff 　    lwr 　　　upr 　　       p adj
B-A   1   -4.2294189    6.229419   0.9252929
C-A   3   -2.2294189    8.229419   0.3245304
D-A   5   -0.2294189  10.229419   0.0609499
C-B   2   -3.2294189    7.229419   0.6297636
D-B   4   -1.2294189    9.229419   0.1441838
D-C   2   -3.2294189    7.229419   0.6297636

有意水準0.05ではどのペアにも差はありませんでした．

T検定でよい？・・・研究目的が重要です

A、B、Cを比較する場合は、単純に多重比較と決めつけてしまうのではなく、求めようとすることを明確にすることが大切です。例えば、「A＞BかつA＞B」を証明するための研究計画であれば、AvsBとAvsBのt検定を行い、両方ともに有意差が言えればよいということになります。

参考　http://www.gen-info.osaka-u.ac.jp/MEPHAS/ave.html
２種類の既存薬ＡとＢを組み合わせた配合薬Ｃの配合効果を評価する場合．この場合、既存薬Ａ，Ｂのそれぞれの効果と配合薬Ｃの効果を比較します．ここで いいたいのはＣが既存薬Ａ、Ｂの両方よりも効果があるということです．「ＣがＡよ りも優れている、かつＣがＢよりも優れている」ということを 示します．つまり帰無仮説はC=AかつC=Bとなり、A=B=Cとは異なります．このような場合には２標本ｔ検定を繰り返して用いるほうが適切だと考えられます．