シミュレーションの準備
まずはforの使い方(なかなか慣れません)
変数xに1から5を足す
0+1+2+3+4+5=15をfor関数で実行
x<-0
for(i in 1:5) x<-x+i
ベクトルに繰り返し数を付ける
x<-c()
i<-c(1,2,3,4,5)
x<-c(x,i)
for関数で実行
x<-c()
for(i in 1:5) x<-c(x,i)
関数として定義すると
myfunc01<-function(){
x<-c()
for(i in 1:5) { # for(i in 1:5){}で{}を5回繰り返す
x<-c(x,i)
}
return(x)
}
myfunc01()
次にif関数の基本です(else ifで条件を増やせます)
coin<-function(){
x<-runif(1) #一様乱数を5個準備
if (x<=1/2) shoubu<-1 #勝負!表=1
else shoubu<-0 #勝負!裏=0
return(shoubu)
}
coin() #表が出たら1、裏が出たら0
上記のcoin関数結果から表回数を集計したらシミュレーションができそうです
count<-0
if(shoubu==1) count<-count+1
coin関数を10回繰り返して、表の出た回数を合計してみます
myfunc02<-function(n){
count<-0
for(i in 1:n){ # for(i in 1:n){}で{}をn回繰り返すことになる
x<-runif(1) #一様乱数を5個準備
if (x<=1/2) shoubu<-1 #勝負!表=1
else shoubu<-0 #勝負!裏=0
if(shoubu==1) count<-count+1 #勝負!表=1ならカウントする
}
return(count)
}
myfunc02(10)
先にcoin関数を定義しておくと
coin<-function(){
x<-runif(1) #一様乱数を準備
if (x<=1/2) shoubu<-1 #勝負!表=1
else shoubu<-0 #勝負!裏=0
return(shoubu)
}
myfunc02を最適化できます
myfunc02<-function(n){
count<-0
for(i in 1:n){ # for(i in 1:n){}で{}をn回繰り返すことになる
x<-runif(1) #一様乱数を準備
count<-count+coin() #勝負!表=1ならカウントする(coin関数)
}
return(count)
}
myfunc02(10)
次回はモンテカルロシミュレーションで近似解を得る関数に挑戦したいと思います!
正規分布から解く
前回の掲載がやや分かりにくい内容でしたので、
r-de-r様からの助言を基に修正しました(2017.6.11)
平均体重がN(70,25^2)に従う集団があります.
その集団から10人ランダムに選択します.
その合計が800㎏を超えてしまう確率は?
求める確率はP(合計≧800)
= P{Z=(合計-700)÷(25*√10)} ≧ {(800-700)÷(25*√10)}
= P(Z ≧ {(800-700)÷(25*√10)})
= P(Z ≧ 1.26)
下図の塗りつぶし部分の確率を求めます
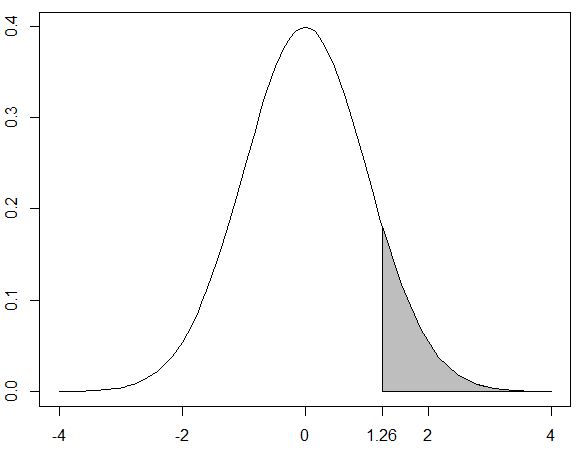
plot(dnorm, -4, 4)
xvals <- seq(1.26, 4, length=10)
# 領域をx軸方向に10個の多角形(台形)に等分割
dvals <- dnorm(xvals)
# 対応するグラフの高さ
polygon(c(xvals,rev(xvals)),c(rep(0,10),rev(dvals)),col="gray")
# 塗りつぶす
axis(side=1,at=c(1.26))
Rで計算してみます
z<-(800-10*70)/(25*sqrt(10)) #Z値(確率点)を算出
1-pnorm(z) #累積分布
pnorm(z, lower.tail=FALSE) #r-de-r様からの助言
=0.1029516
800kgを超える確率は10.1%であると推測できます
N(myu,sd^2)に従う母集団
その集団からn人ランダムに選択します
その合計がmを超えてしまう確率は…
z<-(m-n*myu)/(sd*sqrt(n))
1-pnorm(z) #累積分布
mを超えない確率は…
pnorm(z)
参考)柳川 堯 , 荒木 由布子; バイオ統計の基礎―医薬統計入門,近代科学社 ,2010,p94
確率変数の同時分布
確率変数X、Yの同時分布

出典)柳川 堯 , 荒木 由布子; バイオ統計の基礎―医薬統計入門,近代科学社 ,2010,p60
二次元確率変数の期待値
X=1の周辺分布
P(X=1,Y) = 0.1 + 0.2 = 0.3
確率変数Xの期待値
E(X) = 1*(0.1+0.2) + 2*(0.4+0.3) = 1.7
確率変数Yの期待値
E(Y) = 1*(0.1+0.4) + 2*(0.2+0.3) = 1.5
確率変数X*Yの期待値
E(XY)=1*1*0.1+1*2*0.2+2*1*0.4+2*2*0.3=2.5
XとYの共分散
Cov(X,Y)= E(XY) - E(X) *E(Y) =2.5-1.7*1.5= -0.05
E(X^2)= 1*(0.1+0.2)+ 4*(0.4+0.3) = 3.1
E(Y^2)= 1*(0.1+0.4) + 4*(0.2+0.3) = 2.5
V(X) = E(X^2) – (E(X))^2 = 3.1 - 1.7^2 = 0.21
V(Y) = E(Y^2) – (E(Y))^2 = 2.5 - 1.5^2 = 0.25
V(X+Y) = V(X)+V(Y)+2*Cov(X,Y) = 0.21+0.25+2*(-0.05) = 0.36
共分散と相関係数
(修正日2017.6.5)
何度やっても忘れてしまう(悩)ので、
大切なことは、真面目にコツコツ書くことにしました
たとえばエクセルからコピーしたデータをベクトルにする方法など
x<-read.table("clipboard")
x<-x$V1
これすらも覚えられないので重症(´;ω;`)
共分散
データサンプルwomenを使用しています
x<-women$height
y<-women$weight

#Rの関数で出力
cov(x,y) #=var(x,y) 不偏共分散
cor(x,y) #相関係数
標本から共分散を求める方法(普通の共分散=標本共分散)
mean(x)
mean(y)
sdx<-x-mean(x)
sdy<-y-mean(y)
(sum(sdx*sdy))/length(x) #標本共分散
Rで求めた不偏共分散から標本共分散を求めるためには
(n-1)/nを掛ける
var(x,y)*(length(x)-1)/length(x) #標本共分散
相関係数
cor(x,y) #pearson
cor(x,y,method = "kendall") #kendall
cor(x,y,method = "spearman") #spearman
pearsonの相関係数
共分散÷両テータのの不偏標準偏差
cov(x,y)/(sqrt(var(x))*sqrt(var(y)))
X連鎖劣性遺伝のキャリアの診断
臨床の課題を統計学で読み解く練習
前提)高校の生物学の復習.デュシェンヌ型筋ジストロフィー(Duchenne muscular dystrophy: DMD)はX連鎖劣性遺伝に該当します.母親が保有者、父親が正常である場合に、生まれてくる男児がDMDである確率は0.5となります.ちなみに母親は保有者である確率は、「ある」・「なし」で考えれば0.5になります.
では問題です
Aさん(女性)にはDMDが発症した兄弟がいます.Aさには、夫と二人の息子がいます.夫と二人の息子にはDMDは発症していません.つまり正常です.しかしAさんが検査Tを受けたところDMDのキャリア陽性であることが判明しました.検査Tの感度は0.95、特異度は0.85です.Aさんがキャリアである確率を求めてよ.
ヒント
最終的には検査で陽性だった場合のキャリアである確率を求めます.
P(キャリア│検査陽性)=P(C|T陽)が最終的な答えです.
P(C):キャリアである事前確率
P(N):キャリアでない事前確率
P(T陽|C):キャリアで検査が陽性となる確率(感度)
P(T陽|N):正常で検査が陽性となる確率(偽陽性確率=1‐特異度)
単純に考えるとベイズの定理より
P(C|T陽)={P(T陽|C)P(C)} ÷ {(P(T陽|C)P(C))+(P(T陽|N)P(N))}
を求めればよいのですが、もう一工夫必要になります.
それは、息子が二人とも正常である場合の母親がキャリアである確率を考慮するということです.
つまり P(母親がキャリア|息子二人が正常) という条件付き確率です.
同様にして
P(キャリア│検査陰性)も求めることができます
これは検査が陰性と出たので、母親がキャリアである確率です
つまりキャリアである人を見逃してしまう確率です
ベイズの定理を用いて考えます
ちなみに答えは以下の出典を見て考えましょう.
出典)柳川 堯 , 荒木 由布子; バイオ統計の基礎―医薬統計入門,近代科学社 ,2010,p19-22
ポアソン分布の最尤推定
忘れないうちに書いときます
ポアソン分布とは…
二項分布において、n(→∞)が大きく、p(→0)が小さい場合の確率分布.
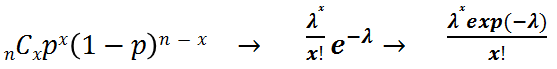
平均1,3,5,7のポアソン分布
y<-0:15
prob<-dpois(y,lambda = 1) #ラムダ=1
plot(y,prob,type = "b",lty=2,xlim=c(0,15),ylim=c(0,0.4),xlab = "",ylab = "")
prob<-dpois(y,lambda = 3)
lines(y,prob,type = "b",lty=2,pch=2)
prob<-dpois(y,lambda = 5)
lines(y,prob,type = "b",lty=2,pch=4)
prob<-dpois(y,lambda = 7)
lines(y,prob,type = "b",lty=2,pch=5)
legend(12,0.35,legend=c("λ=1","λ=3","λ=5","λ=7"),pch = c(1,2,4,5))

ポアソン分布のパラメータλの最尤推定の可視化
準備として平均2.8になるポアソン分布の乱数を50個用意します
x<-rpois(50,2.8)
尤度対数
logL<-function(m)sum(dpois(x,m,log=TRUE))
# 対数尤度関数 sum(dpois(x,m,log=TRUE))
# ポアソン分布の密度関数(dpois)を対数変換(log=TRUE)したもの
lambda<-seq(1,5,0.1)
#λ(平均) 1~5、0.1間隔
plot(lambda,sapply(lambda,logL),type="l",xlab = "λ",ylab = "log likelihood")
#sapply() logLにlambda<-seq(2,5,0.1) を挿入した値を返す
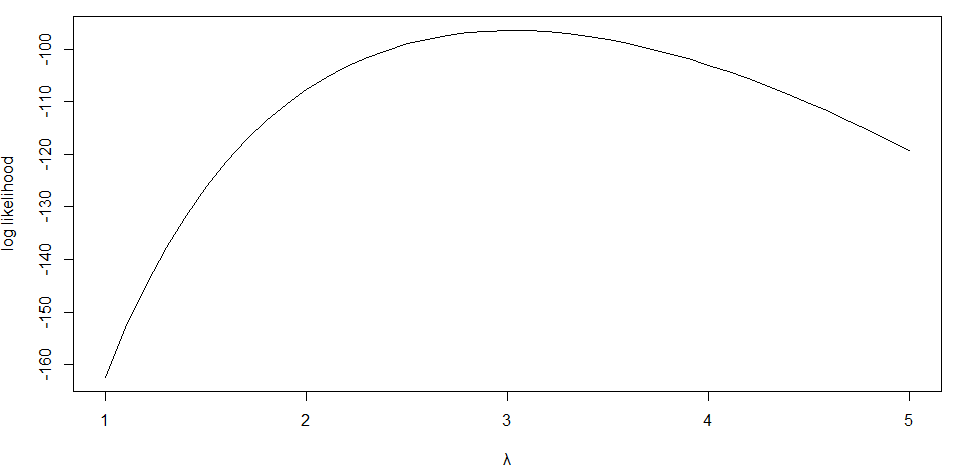
平均2.8になるポアソン分布の乱数なので、もちろん最終推定値は2.8付近になります.
計算では対数尤度関数をλで偏微分して、=0となる値を求めます.
参考資料
久保拓哉:確率分布と一般化線形モデル(GLM)
(http://hosho.ees.hokudai.ac.jp/~kubo/stat/2012/kobe/k2/kubostat2012k2.pdf)