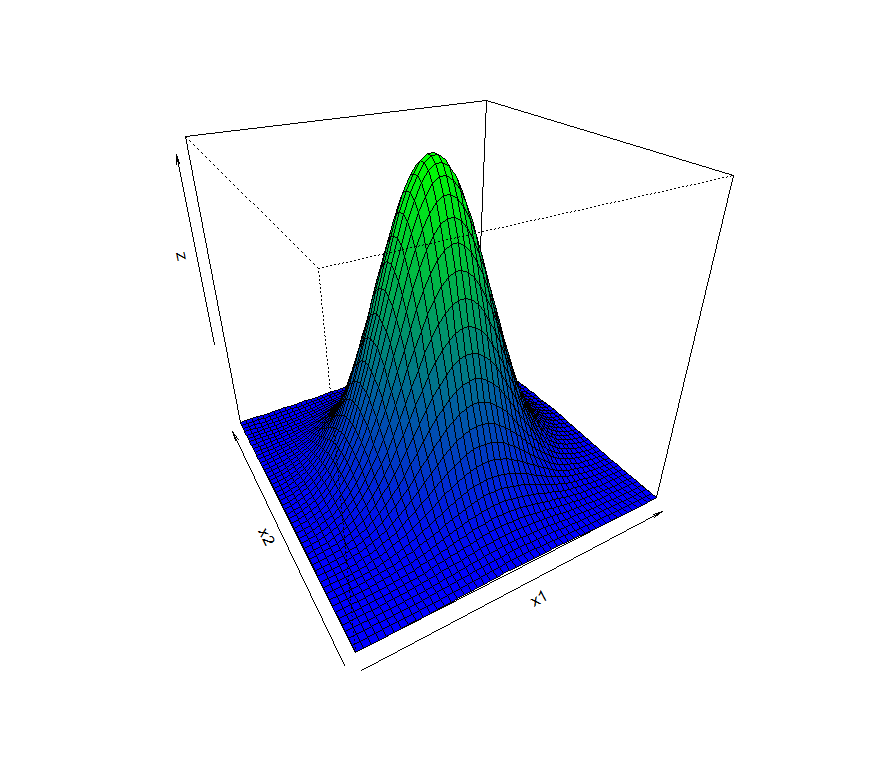
２変量の正規分布をグラフでイメージ（persp）

また、ここで勉強させていただきました．
http://cse.naro.affrc.go.jp/minaka/R/R-binormal.html
忘れないように要点のみ転記させていただます．まさに備忘録．

今回はＲの関数perspを使用して、密度関数の数式から３Ｄのグラフを描いてみます
確率変数ｘ1、ｘ2が正規分布に従い、無相関であることを仮定して進めていきます．

x1 <- seq(-3, 3, length=50)      # -3～3の範囲を50分割

head(x1)  #先頭部分だけ確認してみます
[1] -3.000000 -2.877551 -2.755102 -2.632653 -2.510204 -2.387755

x2 <- x1  

これで変数の設定は完了です．次に、分散1共分散0のマトリックスを作成します．

sigma.zero <- matrix(c(1,0,0,1), ncol=2)

     [,1] [,2]
[1,]    1    0
[2,]    0    1

Ｒの関数functionにｘ1、ｘ2の同時確率密度を定義します． 上記sigma.zeroを分散共分散行列とする密度関数です 　

f <- function(x1,x2) { dmvnorm(matrix(c(x1,x2), ncol=2), mean=c(0,0), sigma=sigma.zero) }

#6ポイントのみ確認してみます
f(-3,-3);f(0,0);f(3,3)
[1] 1.964128e-05
[1] 0.1591549
[1] 1.964128e-05

f(-1,-1);f(0,0);f(1,1)
[1] 0.05854983
[1] 0.1591549
[1] 0.05854983

関数outerを使用して、（x2,x2）であらわされる座標に対しFUN(f <- function(x1,x2))を適用します．
つまり、（x2,x2）に該当する値（f）が定まることになり３次元の描画を可能にします．

z <- outer(x1, x2, f)  
#50×50=2500個のデータが生成されました（length(z)で確認）
#10個だけ見てみましょう
z[1:10]
 [1] 1.964128e-05 2.814820e-05 3.973927e-05 5.526846e-05
 [5] 7.572219e-05 1.022015e-04 1.358875e-04 1.779878e-04
 [9] 2.296621e-04 2.919285e-04

http://cse.naro.affrc.go.jp/minaka/R/R-binormal.html に書かれあります，
z の欠損値の置換は省略しております．
色塗りはＲのヘルプ persp {graphics} をそのまま使用しました．

nrz <- nrow(z)
ncz <- ncol(z)
# Create a function interpolating colors in the range of specified colors
jet.colors <- colorRampPalette( c("blue", "green") )
# Generate the desired number of colors from this palette
nbcol <- 100
color <- jet.colors(nbcol)
# Compute the z-value at the facet centres
zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz]
# Recode facet z-values into color indices
facetcol <- cut(zfacet, nbcol)
persp(x1, x2, z, col = color[facetcol], phi = 30, theta = -30)