信頼区間のプロット

同じサイズのデータサンプルからｔ分布を利用した信頼区間の作図

まずは3×4の場合（サンプルサイズ3を４回実施する）

x <- matrix(NA,nrow=3,ncol=4)        #3×4の空セル

for (i in 1:4){                       #列数分乱数を代入
  x[,i] <- rnorm(3)              #標準正規分布の乱数を行数分繰り返す
}
mx <- rowMeans(x)    #行平均を一括計算
mean(x[1,])                #1行目のみ取り出して確認

vx <- apply(x,1,var)   #行分散を一括計算
var(x[1,])                  #1行目のみ取り出して確認

lx1 <- mx+qt(0.975,2)*sqrt(vx/3)    #95%信頼区間の上限（平均+ｔ値*標準誤差), lower.tail=TRUE 
lx2 <- mx-qt(0.975,2)*sqrt(vx/3)     #95%信頼区間の下限（平均-ｔ値*標準誤差),  (0.975,2, lower.tail=F )=qt(0.025,2,lower.tail=FALSE )

par(mfrow = c(1,2))       #1行2列に図を並べます
plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="")
plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="")
dev.off()          #作図を終了します

#t値はqt(0.025,2)～qt(0.975,2)になります, lower.tail=TRUE 

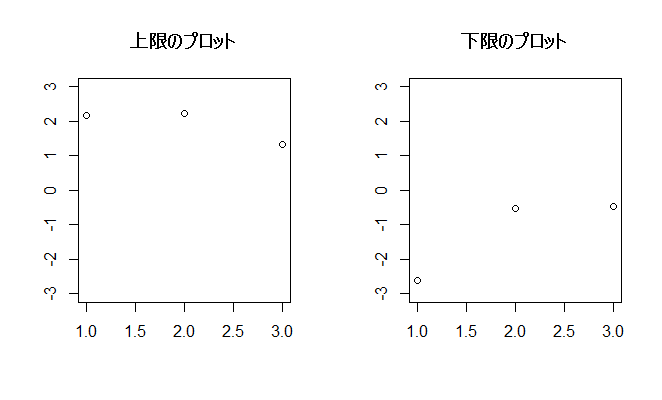
行列数値を増やしていけば見えてきます 1000行10列でやってみます

x <- matrix(NA,nrow=1000,ncol=10)  
for (i in 1:10){   
  x[,i] <- rnorm(1000)   
}
mx <- rowMeans(x) 
vx <- apply(x,1,var) 
lx1 <- mx+qt(0.975,9)*sqrt(vx/10) 
lx2 <- mx-qt(0.975,9)*sqrt(vx/10)
par(mfrow = c(1,2))
plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="")
plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="")
dev.off()

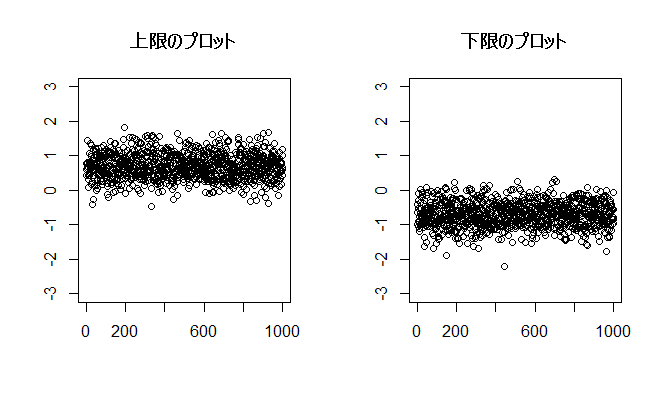
行数＝r,列数＝lとした場合

x <- matrix(NA,nrow=r,ncol=l)  
for (i in 1:l){   
  x[,i] <- rnorm(r)   
}
mx <- rowMeans(x) 
vx <- apply(x,1,var) 
lx1 <- mx+qt(0.975,l-1)*sqrt(vx/l) 
lx2 <- mx-qt(0.975,l-1)*sqrt(vx/l)
par(mfrow = c(1,2))
plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="")
plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="")
dev.off()