統計学的に独立ということ - 統計学備忘録（R言語のメモ）

以前の独立という記事を削除して再投稿

二つの事象A,Bが独立であるということ
一方の事象が起こるかどうかが、他方の事象の起こる確率に影響しないこと
2つの事象AとBが $P(A\cap B)= P(A) \times P(B)$ を満たす場合、事象AとBは統計的に独立である．

このときAとBの余事象も独立である

また

Aの余事象とBの余事象も独立である

条件付き確率
事象A,Bが独立の場合、事象Aと事象Bは互いに影響されないので、
$P(A \mid B)= \frac{P(A\cap B)}{P(B)}=P(A)$
$P(B \mid A)= \frac{P(A\cap B)}{P(A)}=P(B)$
という両式が成立します

例題
2個の大小サイコロを振った場合に、P(A)とP(B)は統計学的に独立か？
事象A（サイコロの和が6）、事象B（大きいサイコロの目が4）の場合

大 <- c(1, 2, 3, 4, 5)
小 <- c(5, 4, 3, 2, 1)
xy <- data.frame(大, 小)

f:id:yoshida931:20171006193628j:plain
$P(A \cap B)=\frac{1}{36}$
$P(A)=\frac{5}{36}$
$P(B)=\frac{1}{6}$
$P(A) \times P(B)=\frac{5}{216}$
$P(A \cap B) \neq P(A) \times P(B)$
したがって事象Aと事象Bは独立ではない

事象A（サイコロの和が7）、事象B（大きいサイコロの目が4）の場合

大 <- c(1, 2, 3, 4, 5, 6)
小 <- c(6, 5, 4, 3, 2, 1)
xy <- data.frame(大, 小)

f:id:yoshida931:20171006194032j:plain
$P(A \cap B)=\frac{1}{36}$
$P(A)=\frac{6}{36}$
$P(B)=\frac{1}{6}$
$P(A) \times P(B)=\frac{6}{216}=\frac{1}{36}$
$P(A \cap B) = P(A) \times P(B)$
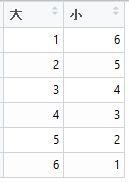
したがって事象Aと事象Bは独立である

ん～なんか不思議な気分ですが…
「統計的独立」当然のことのようにテキストに記載されていることでありますが、
実に意義深く重要なことのように思えます…
もうちっと掘り下げねば…

柳川堯 , 荒木由布子; バイオ統計の基礎―医薬統計入門,近代科学社 ,2010,p235