ファイ係数

連関係数
　クロス集計表における2つの変数間の関連性の程度を表す指標として，連関係数が提案されています．

連関係数＜｜0.2｜　連関はほとんどない
｜0.2｜≦連関係数＜｜0.4｜　やや連関がある
｜0.4｜≦連関係数＜｜0.7｜　強い連関がある
｜0.7｜≦連関係数　かなり強い連関がある
　　　対馬栄輝; よくわかる医療統計 -「なぜ?」にこたえる道しるべ, 東京図書, 2015

ファイ係数 (φ係数)
　クロス集計表における行要素と列要素の関連の強さを示す指標. 1と0の2つの値からなる変数に対して計算される相関係数です。つまり、２つの２値変数をそれぞれ1と0で数値化した上で算出した積率相関係数です。1と0の2つの値とは、「好き、嫌い」、「はい、いいえ」など、2択で表現されるデータです. 選択肢Aに0を、選択肢Bに1を割り付けることで、ファイ係数を求めることができます.

例）2つの質問 ( q1 , q2 ) に関する答え ( yes , no ) のベクトルを考えます．
q1<-c("yes","yes","yes","yes","yes","yes","yes","no","no","no")
q2<-c("yes","yes","yes","no","no","no","no","yes","yes","no")
q101<-ifelse(q1=="yes",1,0)        # 0,1のベクトルに変更
  q101 <- c(1, 1, 1, 1, 1, 1, 1, 0, 0, 0)
q201<-ifelse(q2=="yes",1,0)       # 0,1のベクトルに変更
  q201 <- c(1, 1, 1, 0, 0, 0, 0, 1, 1, 0)

ピアソンの積率相関係数を2行×2列のクロス集計表に適用したもの
　　　ピアソンの積率相関係数

           

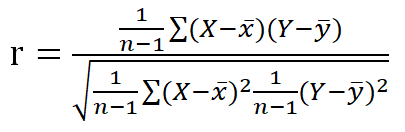
mean ( q101 )
=0.7
mean ( q201 )
=0.5
sum ( ( q101-0.7 ) * ( q201 - 0.5 ) )
= - 0.5
sum ( ( q101 - 0.7 )^2 )
=2.1
sum ( ( q201 - 0.5 )^2 )
=2.5
r = - 0.5 / sqrt ( 2.1 * 2.5 )
  = - 0.2182179

Rの関数で確認してみます
cor(q101,q201)                #相関係数をcor( )で算出
= - 0.2182179

次に例題をテーブルにして眺めてみます
tq<- table ( q1,q2 )　   

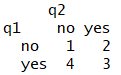
t<- tq [ c(2,1) , c(2,1) ] 　　
#これは不要ですがラベルの並べ替えです．yesから始めたいので挿入しておきます（1番目と2番目の入れ替え）

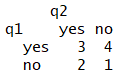
理解のためにデータフレームに変換します
t< - data.frame ( t )       

 
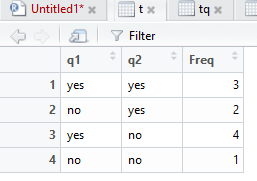
     q1   q2    Freq
1   yes  yes   3         #  t $ Freq[1]
2   no    yes   2        #  t $ Freq[2]
3   yes   no    4        #  t $ Freq[3]
4   no    no     1        #  t $ Freq[4]

ファイ係数φその1　ｶｲ二乗値より
φ＝√（ｶｲ二乗値/ｎ）
chisq.test ( tq , correct=F )
X-squared = 0.47619
φ＝sqrt ( 0.47619 / 10 )
= 0.2182178

ファイ係数φその2  観測値と周辺度数より

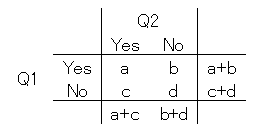
φ =  ( a*d - b*c ) / √ ( a+b )*( c+d )*( a+c )*( b+d )*
x <- t$Freq[1] * t$Freq[4] - t$Freq[2] * t$Freq[3]　  # x = 対角線上の観測値を掛けたものの差
y <- ( t$Freq[1] + t$Freq[3] )* 　                               # y = 全ての周辺度数を掛けたもの
  ( t$Freq[2] + t$Freq[4] )*
  ( t$Freq[1] + t$Freq[2] )*
  ( t$Freq[3] + t$Freq[4] )
φ ＝ x / sqrt(y)
    = - 0.2182179

Rの関数で確認してみます
install.packages ( "psych" )
library ( psych ) 
phi ( tq , digits=8 )
= - 0.2182179