正規分布から解く
前回の掲載がやや分かりにくい内容でしたので、
r-de-r様からの助言を基に修正しました(2017.6.11)
平均体重がN(70,25^2)に従う集団があります.
その集団から10人ランダムに選択します.
その合計が800㎏を超えてしまう確率は?
求める確率はP(合計≧800)
= P{Z=(合計-700)÷(25*√10)} ≧ {(800-700)÷(25*√10)}
= P(Z ≧ {(800-700)÷(25*√10)})
= P(Z ≧ 1.26)
下図の塗りつぶし部分の確率を求めます
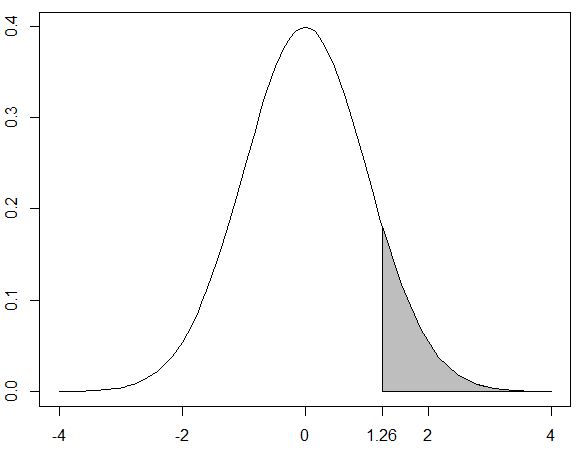
plot(dnorm, -4, 4)
xvals <- seq(1.26, 4, length=10)
# 領域をx軸方向に10個の多角形(台形)に等分割
dvals <- dnorm(xvals)
# 対応するグラフの高さ
polygon(c(xvals,rev(xvals)),c(rep(0,10),rev(dvals)),col="gray")
# 塗りつぶす
axis(side=1,at=c(1.26))
Rで計算してみます
z<-(800-10*70)/(25*sqrt(10)) #Z値(確率点)を算出
1-pnorm(z) #累積分布
pnorm(z, lower.tail=FALSE) #r-de-r様からの助言
=0.1029516
800kgを超える確率は10.1%であると推測できます
N(myu,sd^2)に従う母集団
その集団からn人ランダムに選択します
その合計がmを超えてしまう確率は…
z<-(m-n*myu)/(sd*sqrt(n))
1-pnorm(z) #累積分布
mを超えない確率は…
pnorm(z)
参考)柳川 堯 , 荒木 由布子; バイオ統計の基礎―医薬統計入門,近代科学社 ,2010,p94