Rで簡単（ｔ検定の検定力分析）

パッケージpwrを使用します
library(pwr)

pwr.t.test(n = , d = , sig.level = , power = , type = c("two.sample", "one.sample", "paired"))
n=標本数
d=効果量（）
sig.level=有意水準
power=検定力
type=t検定の形（"two.sample=対応なし", "one.sample=1標本", "paired=対応あり"）

n, d, power, and sig.level のいずれかを空白(NULL)にします
strict=T   #厳密な検定が可能になる
　（効果量(effect size)のはなし - 六本木で働くデータサイエンティストのブログ）

必要な標本数を求めてみます
pwr.t.test(n =NULL, d =0.2 , sig.level =0.05 , power = 0.8, type ="two.sample")

Two-sample t test power calculation

n = 393.4057
d = 0.2
sig.level = 0.05
power = 0.8
alternative = two.sided

効果量0.2、有意水準0.05、検定力0.8の場合の標本の大きさは393必要になります
もちろんフリーソフトG＊powerを使用した結果と同じになります

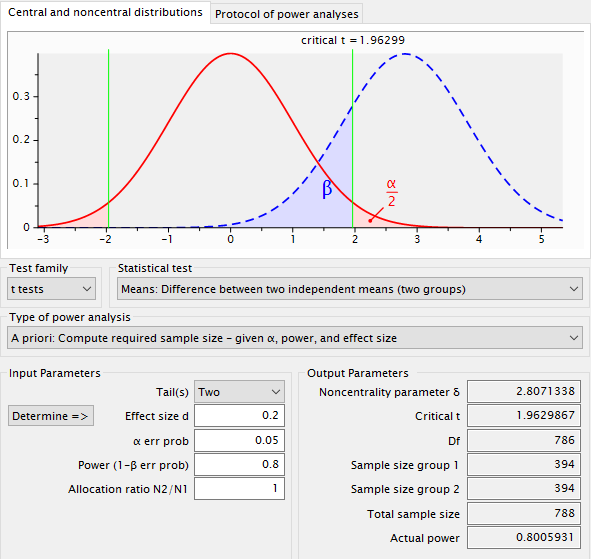
効果量をもとめてみます
pwr.t.test(n =150, d =NULL , sig.level =0.05 , power = 0.8, type ="two.sample")

Two-sample t test power calculation

n = 150
d = 0.3245459
sig.level = 0.05
power = 0.8
alternative = two.sided

標本数150、有意水準0.05、検定力0.8の場合の効果量は0.32と低くなります
フリーソフトG＊powerを使用した結果

Rの予備知識
for(i in c(2,4,6)) でiに2,4,6を順に挿入する命令
print(･･･)　引数が数値ベクトルの場合にはベクトルの中身を表示する
print(c(1,2,3))
合わせて
for(i in c(0.26,0.24,0.22)){print(x<-c(i+1))}
round 四捨五入を導入して･･･
for(i in c(0.26,0.24,0.22)){print(round(x<-c(i+1),1))}

上記を利用して
有意水準が.05,.01,.001)のときの対応なしｔ検定のpowerを一気に算出してみます
pwr.t.test(n =NULL,d =0.2,sig.level=0.05,power=0.8,type ="two.sample")
for(i in c(.05,.01,.001)){print(round(pwr.t.test(n =394,d =0.2,sig.level=i,
,type ="two.sample")$power,2))}

[1] 0.8
[1] 0.59
[1] 0.31

対応のなし（2群の標本数が異なる場合）
pwr.t2n.test(n1 = , n2= , d = , sig.level =, power = )
例）
pwr.t2n.test(n1 =120, n2=NULL , d =0.5 , sig.level =0.05, power =0.8 )

t test power calculation

n1 = 120
n2 = 43.21666
d = 0.5
sig.level = 0.05
power = 0.8
alternative = two.sided

n1=120、効果量0.5、有意水準0.05、検定力0.8、両側検定の場合n1=43.2必要