Rで簡単 多重ロジスティック回帰分析
下記のサイトに移転いたしました
変数の呼称について(目的変数と説明変数)
それぞれの研究界のご意見はあると思うのですが・・・
ややこしや
目的変数  は以下のように呼ばれています
は以下のように呼ばれています
目的変数 objective variable
応答変数 response variable
反応変数 reaction variable(response variable )
結果変数 outcome variable
従属変数 dependent variable
基準変数 criterion variable
外的基準 external criterion
被説明変数 explained variable
説明変数  は以下のように呼ばれています
は以下のように呼ばれています
説明変数 explanatory variable
予測変数 predictor variable
独立変数 independent variable
パターンとしては
「目的変数&説明変数」
「従属変数&独立変数」
「被説明変数&説明変数」
個人的には…
応答変数&説明変数が理解しやすいかな?
2変量の正規分布をグラフでイメージ(persp)
また、ここで勉強させていただきました.
http://cse.naro.affrc.go.jp/minaka/R/R-binormal.html
忘れないように要点のみ転記させていただます.まさに備忘録.
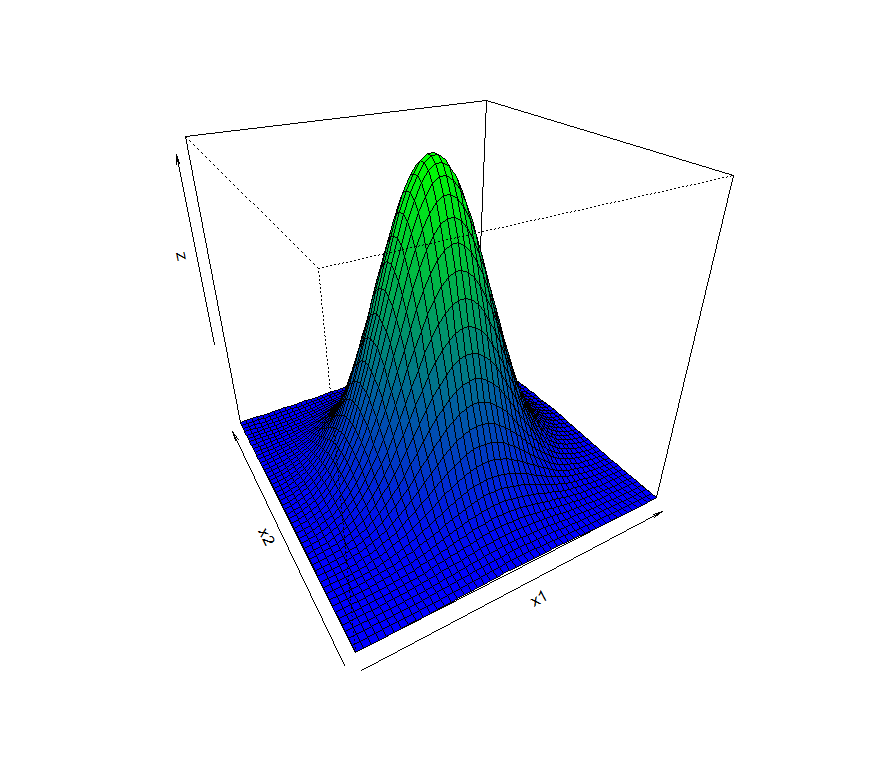
今回はRの関数perspを使用して、密度関数の数式から3Dのグラフを描いてみます
確率変数x1、x2が正規分布に従い、無相関であることを仮定して進めていきます.
x1 <- seq(-3, 3, length=50) # -3~3の範囲を50分割 head(x1) #先頭部分だけ確認してみます [1] -3.000000 -2.877551 -2.755102 -2.632653 -2.510204 -2.387755 x2 <- x1
これで変数の設定は完了です.次に、分散1共分散0のマトリックスを作成します.
sigma.zero <- matrix(c(1,0,0,1), ncol=2) [,1] [,2] [1,] 1 0 [2,] 0 1
Rの関数functionにx1、x2の同時確率密度を定義します. 上記sigma.zeroを分散共分散行列とする密度関数です
f <- function(x1,x2) { dmvnorm(matrix(c(x1,x2), ncol=2), mean=c(0,0), sigma=sigma.zero) } #6ポイントのみ確認してみます f(-3,-3);f(0,0);f(3,3) [1] 1.964128e-05 [1] 0.1591549 [1] 1.964128e-05 f(-1,-1);f(0,0);f(1,1) [1] 0.05854983 [1] 0.1591549 [1] 0.05854983
関数outerを使用して、(x2,x2)であらわされる座標に対しFUN(f <- function(x1,x2))を適用します.
つまり、(x2,x2)に該当する値(f)が定まることになり3次元の描画を可能にします.
z <- outer(x1, x2, f) #50×50=2500個のデータが生成されました(length(z)で確認) #10個だけ見てみましょう z[1:10] [1] 1.964128e-05 2.814820e-05 3.973927e-05 5.526846e-05 [5] 7.572219e-05 1.022015e-04 1.358875e-04 1.779878e-04 [9] 2.296621e-04 2.919285e-04
http://cse.naro.affrc.go.jp/minaka/R/R-binormal.html に書かれあります,
z の欠損値の置換は省略しております.
色塗りはRのヘルプ persp {graphics} をそのまま使用しました.
nrz <- nrow(z) ncz <- ncol(z) # Create a function interpolating colors in the range of specified colors jet.colors <- colorRampPalette( c("blue", "green") ) # Generate the desired number of colors from this palette nbcol <- 100 color <- jet.colors(nbcol) # Compute the z-value at the facet centres zfacet <- z[-1, -1] + z[-1, -ncz] + z[-nrz, -1] + z[-nrz, -ncz] # Recode facet z-values into color indices facetcol <- cut(zfacet, nbcol) persp(x1, x2, z, col = color[facetcol], phi = 30, theta = -30)
2変量の正規分布をグラフでイメージ(scatterplot3d)
ここで勉強させていただきました.
http://cse.naro.affrc.go.jp/minaka/R/R-binormal.html
忘れないように要点のみ転記させていただます.
必要なパッケージをインストールします
install.packages("mvtnorm") library(mvtnorm) install.packages("scatterplot3d") library(scatterplot3d)
パッケージmvtnormは以下を参照
yoshida931.hatenablog.com
次に散布図を描きます
#共分散が0なので2変数には相関がありません sigma.zero <- matrix(c(1,0,0,1), ncol=2) [,1] [,2] [1,] 1 0 [2,] 0 1 #ともに平均=0,共分散=0となる2変数(乱数)を3組生成(n=100, n=1000, n=10000) x100 <- rmvnorm(n=100, mean=c(0,0), sigma=sigma.zero) x1000 <- rmvnorm(n=1000, mean=c(0,0), sigma=sigma.zero) x10000 <- rmvnorm(n=10000, mean=c(0,0), sigma=sigma.zero) #3組並べて散布図 par(mfrow = c(1,3)) plot(x100) plot(x1000) plot(x10000)

確かに共分散はゼロです.
par(mfrow = c(1,3)) scatterplot3d(x100[,1], x100[,2], dmvnorm(x100, mean=c(0,0), sigma=sigma.zero), highlight=TRUE) scatterplot3d(x1000[,1], x1000[,2], dmvnorm(x1000, mean=c(0,0), sigma=sigma.zero), highlight=TRUE) scatterplot3d(x10000[,1], x10000[,2], dmvnorm(x10000, mean=c(0,0), sigma=sigma.zero), highlight=TRUE)

逆関数のグラフ
の逆関数は
y <- function(x){ x } y1 <- function(x){ 2*x-2 } y2 <- function(x){ (x+2)/2 } plot(y,xlim = c(-2,4),ylim=c(-2,4),col=2,ann=FALSE, axes=FALSE) #ann軸ラベル axes軸 par(new=T) plot(y1,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) par(new=T) plot(y2,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) axis(1, pos = 0, at = -2:4) #軸挿入 axis(2, pos = 0, at = -2:4)

の逆関数は
y <- function(x){ x } y1 <- function(x){ 10^x } y2 <- function(x){ log10(x) } plot(y,xlim = c(-2,4),ylim=c(-2,4),col=2,ann=FALSE, axes=FALSE) #ann軸ラベル axes軸 par(new=T) plot(y1,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) par(new=T) plot(y2,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) axis(1, pos = 0, at = -2:4) #軸挿入 axis(2, pos = 0, at = -2:4)

分散共分散行列 相関のあるサンプル作成
データセットから分散共分散行列を求めてみます
x1 <- c(151, 164, 146, 158) x2 <- c(48, 53, 45, 61) x3 <- c(8, 11, 8, 9) data <- data.frame(x1,x2,x3) #分散共分散行列 var(data) x1 x2 x3 x1 62.25000 38.250000 10.333333 x2 38.25000 48.916667 4.333333 x3 10.33333 4.333333 2.000000 #相関行列 cor(data) x1 x2 x3 x1 1.0000000 0.6931597 0.9260955 x2 0.6931597 1.0000000 0.4381055 x3 0.9260955 0.4381055 1.0000000
定義に従って相関係数を求めてみます. 例)cor(data)[2]を算出してみます
cor(data)[2] var(data)[2]/sqrt(var(data)[1]*var(data)[5])
シミュレーション
平均や分散を指定した乱数を作成するのは簡単です.例えば正規分布であればrnorm(10,5,3)で、平均5分散9の乱数が10個生成されます.
しかし繰り返しデータの場合に、それぞれの回数の相関を設定した乱数を作成するのはちょっと難しくなります.
5回繰り返しデータ(X1~X5)を想定します.また、それぞれの平均値が(0,3,5,-2,-1)、分散8、共分散3となるように乱数を発生させます.
#まず、次のような共分散行列を作成します x1 x2 x3 x4 x5 x1 8 3 3 3 3 x2 3 8 3 3 3 x3 3 3 8 3 3 x4 3 3 3 8 3 x5 3 3 3 3 8 sigma <- matrix(rep(6,25),ncol = 5) # 3を25個作成 sigma [,1] [,2] [,3] [,4] [,5] [1,] 6 6 6 6 6 [2,] 6 6 6 6 6 [3,] 6 6 6 6 6 [4,] 6 6 6 6 6 [5,] 6 6 6 6 6 #次に分散8を挿入します diag(sigma)=rep(8,5) #斜めに挿入 sigma [,1] [,2] [,3] [,4] [,5] [1,] 8 6 6 6 6 [2,] 6 8 6 6 6 [3,] 6 6 8 6 6 [4,] 6 6 6 8 6 [5,] 6 6 6 6 8 #X1~X5の平均値を設定します m <- c(0, 3, 5, -2, -1) #パッケージをインストールします install.packages("mvtnorm") library(mvtnorm) #平均m, 分散8, 共分散3になるようなX1~X5を10組の乱数を発生させます. y <- rmvnorm(10, m, sigma, method = "chol") #乱数 colnames(y) <- name #イメージのために書き出しておきます.乱数なので算出毎に数値は変化します. y x1 x2 x3 x4 x5 [1,] 3.52189310 6.3816131 8.5906099 0.3448154 2.4660227 [2,] 0.92752113 4.9547725 7.9595828 0.3717669 1.3875238 [3,] -5.19449966 -0.3019742 -1.4509597 -4.3760477 -5.0233539 [4,] -1.01591408 4.2919216 5.4850598 -1.0672082 -1.4707111 [5,] -3.80629633 -0.6012603 4.7040327 -6.4885712 -3.7804199 [6,] -3.10433704 5.7128433 2.2531806 -1.1011307 0.8055750 [7,] 2.05904069 4.8775650 6.2192196 0.3335801 0.4234229 [8,] -0.62623689 4.2532797 3.7670864 -1.5564523 -1.8985524 [9,] -0.09027824 3.3205490 5.0517354 -1.2558948 -1.0637946 [10,] -1.30173038 -3.0114726 0.8776159 -8.0027438 -3.9780232 #各列に適当に色をつけて、プロットしてくれるmatplotを使って、作図します. #デフォルトでは col の順番なのでx1=黒 ,x2=赤, x3=緑, x4=青, x5=水色 matplot(y,type="l")

互いに相関のある群(相関係数0.75)を作成
#分散共分散行列よりそれぞれの相関係数は、6/√8*√8=0.75 が読み取れます x1 x2 x3 x4 x5 x1 8 3 3 3 3 x2 3 8 3 3 3 x3 3 3 8 3 3 x4 3 3 3 8 3 x5 3 3 3 3 8
しかしグラフからは、X1~X5の相関が理解できません.
ここからは、上記yをコピーしたy2を使用して進めていきます.
相関行列を確認してみたら6/√8*√8=0.75に近い相関になっています.
cor(y2) x1 x2 x3 x4 x5 x1 1.0000000 0.6014473 0.8170968 0.6413491 0.7693525 x2 0.6014473 1.0000000 0.6684236 0.9623296 0.8923660 x3 0.8170968 0.6684236 1.0000000 0.6635989 0.7835190 x4 0.6413491 0.9623296 0.6635989 1.0000000 0.8511389 x5 0.7693525 0.8923660 0.7835190 0.8511389 1.0000000
nのサイズを大きくすれば、相関係数はさらに6/√8*√8=0.75に近づきます
y3 <- rmvnorm(50, m, sigma, method = "chol") cor(y3) [,1] [,2] [,3] [,4] [,5] [1,] 1.0000000 0.8068844 0.7566464 0.7541858 0.7390697 [2,] 0.8068844 1.0000000 0.7345947 0.6725027 0.6586652 [3,] 0.7566464 0.7345947 1.0000000 0.7810799 0.7455624 [4,] 0.7541858 0.6725027 0.7810799 1.0000000 0.7226452 [5,] 0.7390697 0.6586652 0.7455624 0.7226452 1.0000000
y3をグラフにしてみます
matplot(y3,type="l")

x軸をX1~X5に移行することで相関が可視化できます
matplot(t(y3),type="l")

x1~x5まで、ほぼ同じ範囲に入っており相関の強さが視覚的に確認できました
復習のためにy3を残しておきます
[,1] [,2] [,3] [,4] [,5] [1,] 0.10151443 2.499704243 5.9057675 -3.4943595 -1.3900978 [2,] 1.50663613 5.280020390 6.0871375 -1.6427891 4.1792270 [3,] 5.15807547 9.240978804 10.1524971 1.6396755 4.2384627 [4,] 0.52636740 7.362142992 8.2131410 -2.7272272 -0.1657287 [5,] -1.82768487 2.078275786 4.8978490 -1.3363880 -2.6741024 [6,] 4.43524347 8.060044313 8.8144178 2.4425139 2.0623879 [7,] 0.37328244 5.317456919 3.7818383 -1.0436226 -0.7600355 [8,] -4.91121977 -0.627691232 3.4766397 -4.2966815 -1.9693309 [9,] 3.08701302 4.490715808 8.0062255 1.3102477 3.4494656 [10,] -1.07464046 4.124389139 4.1597881 -3.2331504 -1.5478108 [11,] -4.98187707 -2.960175387 -1.1852294 -8.4042762 -6.7175592 [12,] 0.55455335 4.811030651 4.4954359 -2.1924783 -1.6559525 [13,] -3.25343072 0.216598109 2.5139412 -4.0381462 -2.4717920 [14,] 0.71190379 0.664704194 7.4396890 1.2862593 -0.7421359 [15,] 2.05860252 2.432888164 3.5347403 -1.8087834 -1.5556714 [16,] -4.35657559 0.316841111 1.6688628 -5.3447686 -4.5653558 [17,] 0.52655249 0.326658121 3.3274462 -5.0033717 -1.4797982 [18,] -0.51997740 1.522057422 3.9754390 -2.2568758 -3.4186446 [19,] -2.48896458 0.609983346 4.4815961 -4.4651604 0.5507060 [20,] -1.27166463 0.860673117 4.5316817 -1.6695152 -1.5116476 [21,] 2.36579566 8.115692097 10.1842162 1.5469158 1.2745295 [22,] -2.61885567 2.264994539 1.8073273 -4.6059818 -5.2668700 [23,] -2.87195778 -0.354779514 4.4273497 -2.1824915 -2.3847656 [24,] -0.31689104 4.490830114 7.2127744 0.8737950 3.2108026 [25,] 0.86603870 3.574589801 4.4276743 -1.6189355 -0.6536883 [26,] -1.08641447 1.650209214 0.2495224 -3.6113148 -3.8762204 [27,] -1.06718456 1.333869467 2.7389823 -6.0151694 -1.0285024 [28,] 2.92878284 3.572365454 7.5983883 4.4834977 1.1370509 [29,] 1.25628266 3.077046228 4.4049753 -3.9389680 0.8752170 [30,] -2.25266309 1.031792708 2.0312006 -5.2208742 -1.1417857 [31,] -1.83386252 1.464612026 5.4984764 -2.5442451 -2.5926546 [32,] -3.74237017 0.948552374 1.6345401 -5.3518601 -4.3701054 [33,] 1.57641371 2.949825751 7.6793848 2.8385187 2.5930688 [34,] -1.70707918 4.328429267 4.8674954 -2.3957196 -0.6474211 [35,] -0.68729957 0.186676655 6.3561554 -4.9844379 -2.6635800 [36,] -5.70176744 0.002329385 3.3561491 -3.6218192 -2.5791208 [37,] 0.73014712 2.200125852 3.0212866 -1.4821494 -3.4750934 [38,] 2.51743524 4.256512695 3.2907951 1.0304869 3.3052088 [39,] -3.71975203 -0.761618136 3.5496253 -2.0532424 -1.8430078 [40,] 4.00292393 6.456935876 9.6564018 1.9699281 0.9976009 [41,] -0.76466675 5.343766540 4.4333739 -0.7760534 -1.2543057 [42,] -5.23139631 -2.144231142 0.3253171 -7.3690128 -5.2907999 [43,] 0.22047353 0.598735545 5.6964360 -3.8599177 0.1664410 [44,] 0.25324554 4.186434455 3.3374806 -2.2359334 -2.5759674 [45,] -0.33142225 3.259191383 4.9409355 -4.1641440 -3.3400309 [46,] 4.28859451 7.946808493 9.4197735 1.7908695 1.2385851 [47,] 0.91987986 4.440995369 4.2562333 -4.3308892 -1.1173378 [48,] -3.44169133 0.376280288 2.3650166 -3.1425327 -3.2670228 [49,] 0.07415149 2.969230453 5.1548999 -1.9221235 2.5954580 [50,] 2.51582740 4.186680476 6.5627895 1.7226084 3.3340985
データ取り込みと保存
クリップボードから一覧表の形式に取り込み
エクセルなどの一覧表から必要な部分をコピーします.

その後、いかのような操作でRに取り込むことができます.
#x のなかに一覧表として取り込みます x <- read.table("clipboard",header = T) #xを確認すると ID A B C 1 x1 10.5 8.9 9.9 2 x2 11.2 9.9 10.6 3 x3 9.5 10.2 11.5 4 x4 10.6 8.5 12.3 5 x5 12.3 13.2 11.3 #x2のなかに1列目のIDを行名として取り込む場合 x2 <- read.table("clipboard",header = T, row.names=1) #x2を確認するとIDというラベルが消えて、IDは行名として扱われます A B C x1 10.5 8.9 9.9 x2 11.2 9.9 10.6 x3 9.5 10.2 11.5 x4 10.6 8.5 12.3 x5 12.3 13.2 11.3
列の取り出し
x2のなかのAとBをそれぞれ取り出します
x2$A [1] 10.5 11.2 9.5 10.6 12.3 x2$B [1] 8.9 9.9 10.2 8.5 13.2
取り出したAとBをt検定してみます
t.test(x2$A,x2$B) Welch Two Sample t-test data: x2$A and x2$B t = 0.71918, df = 6.2608, p-value = 0.498 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.610436 2.970436 sample estimates: mean of x mean of y 10.82 10.14
cvsファイルからの取り込み
あらかじめ作業ディレクトリにファイルを保管しておく必要があります.
y <- read.csv("sample01.csv",row.names=1)
データの保存
取り込んだyの一覧表を、テキストとして作業ディレクトリに保存してみます
write.table(y,file = "data.txt") #dataというテキストファイルが作成されます