逆関数のグラフ
の逆関数は
y <- function(x){ x } y1 <- function(x){ 2*x-2 } y2 <- function(x){ (x+2)/2 } plot(y,xlim = c(-2,4),ylim=c(-2,4),col=2,ann=FALSE, axes=FALSE) #ann軸ラベル axes軸 par(new=T) plot(y1,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) par(new=T) plot(y2,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) axis(1, pos = 0, at = -2:4) #軸挿入 axis(2, pos = 0, at = -2:4)

の逆関数は
y <- function(x){ x } y1 <- function(x){ 10^x } y2 <- function(x){ log10(x) } plot(y,xlim = c(-2,4),ylim=c(-2,4),col=2,ann=FALSE, axes=FALSE) #ann軸ラベル axes軸 par(new=T) plot(y1,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) par(new=T) plot(y2,xlim = c(-2,4),ylim=c(-2,4),ann=FALSE, axes=FALSE) axis(1, pos = 0, at = -2:4) #軸挿入 axis(2, pos = 0, at = -2:4)

分散共分散行列 相関のあるサンプル作成
データセットから分散共分散行列を求めてみます
x1 <- c(151, 164, 146, 158) x2 <- c(48, 53, 45, 61) x3 <- c(8, 11, 8, 9) data <- data.frame(x1,x2,x3) #分散共分散行列 var(data) x1 x2 x3 x1 62.25000 38.250000 10.333333 x2 38.25000 48.916667 4.333333 x3 10.33333 4.333333 2.000000 #相関行列 cor(data) x1 x2 x3 x1 1.0000000 0.6931597 0.9260955 x2 0.6931597 1.0000000 0.4381055 x3 0.9260955 0.4381055 1.0000000
定義に従って相関係数を求めてみます. 例)cor(data)[2]を算出してみます
cor(data)[2] var(data)[2]/sqrt(var(data)[1]*var(data)[5])
シミュレーション
平均や分散を指定した乱数を作成するのは簡単です.例えば正規分布であればrnorm(10,5,3)で、平均5分散9の乱数が10個生成されます.
しかし繰り返しデータの場合に、それぞれの回数の相関を設定した乱数を作成するのはちょっと難しくなります.
5回繰り返しデータ(X1~X5)を想定します.また、それぞれの平均値が(0,3,5,-2,-1)、分散8、共分散3となるように乱数を発生させます.
#まず、次のような共分散行列を作成します x1 x2 x3 x4 x5 x1 8 3 3 3 3 x2 3 8 3 3 3 x3 3 3 8 3 3 x4 3 3 3 8 3 x5 3 3 3 3 8 sigma <- matrix(rep(6,25),ncol = 5) # 3を25個作成 sigma [,1] [,2] [,3] [,4] [,5] [1,] 6 6 6 6 6 [2,] 6 6 6 6 6 [3,] 6 6 6 6 6 [4,] 6 6 6 6 6 [5,] 6 6 6 6 6 #次に分散8を挿入します diag(sigma)=rep(8,5) #斜めに挿入 sigma [,1] [,2] [,3] [,4] [,5] [1,] 8 6 6 6 6 [2,] 6 8 6 6 6 [3,] 6 6 8 6 6 [4,] 6 6 6 8 6 [5,] 6 6 6 6 8 #X1~X5の平均値を設定します m <- c(0, 3, 5, -2, -1) #パッケージをインストールします install.packages("mvtnorm") library(mvtnorm) #平均m, 分散8, 共分散3になるようなX1~X5を10組の乱数を発生させます. y <- rmvnorm(10, m, sigma, method = "chol") #乱数 colnames(y) <- name #イメージのために書き出しておきます.乱数なので算出毎に数値は変化します. y x1 x2 x3 x4 x5 [1,] 3.52189310 6.3816131 8.5906099 0.3448154 2.4660227 [2,] 0.92752113 4.9547725 7.9595828 0.3717669 1.3875238 [3,] -5.19449966 -0.3019742 -1.4509597 -4.3760477 -5.0233539 [4,] -1.01591408 4.2919216 5.4850598 -1.0672082 -1.4707111 [5,] -3.80629633 -0.6012603 4.7040327 -6.4885712 -3.7804199 [6,] -3.10433704 5.7128433 2.2531806 -1.1011307 0.8055750 [7,] 2.05904069 4.8775650 6.2192196 0.3335801 0.4234229 [8,] -0.62623689 4.2532797 3.7670864 -1.5564523 -1.8985524 [9,] -0.09027824 3.3205490 5.0517354 -1.2558948 -1.0637946 [10,] -1.30173038 -3.0114726 0.8776159 -8.0027438 -3.9780232 #各列に適当に色をつけて、プロットしてくれるmatplotを使って、作図します. #デフォルトでは col の順番なのでx1=黒 ,x2=赤, x3=緑, x4=青, x5=水色 matplot(y,type="l")

互いに相関のある群(相関係数0.75)を作成
#分散共分散行列よりそれぞれの相関係数は、6/√8*√8=0.75 が読み取れます x1 x2 x3 x4 x5 x1 8 3 3 3 3 x2 3 8 3 3 3 x3 3 3 8 3 3 x4 3 3 3 8 3 x5 3 3 3 3 8
しかしグラフからは、X1~X5の相関が理解できません.
ここからは、上記yをコピーしたy2を使用して進めていきます.
相関行列を確認してみたら6/√8*√8=0.75に近い相関になっています.
cor(y2) x1 x2 x3 x4 x5 x1 1.0000000 0.6014473 0.8170968 0.6413491 0.7693525 x2 0.6014473 1.0000000 0.6684236 0.9623296 0.8923660 x3 0.8170968 0.6684236 1.0000000 0.6635989 0.7835190 x4 0.6413491 0.9623296 0.6635989 1.0000000 0.8511389 x5 0.7693525 0.8923660 0.7835190 0.8511389 1.0000000
nのサイズを大きくすれば、相関係数はさらに6/√8*√8=0.75に近づきます
y3 <- rmvnorm(50, m, sigma, method = "chol") cor(y3) [,1] [,2] [,3] [,4] [,5] [1,] 1.0000000 0.8068844 0.7566464 0.7541858 0.7390697 [2,] 0.8068844 1.0000000 0.7345947 0.6725027 0.6586652 [3,] 0.7566464 0.7345947 1.0000000 0.7810799 0.7455624 [4,] 0.7541858 0.6725027 0.7810799 1.0000000 0.7226452 [5,] 0.7390697 0.6586652 0.7455624 0.7226452 1.0000000
y3をグラフにしてみます
matplot(y3,type="l")

x軸をX1~X5に移行することで相関が可視化できます
matplot(t(y3),type="l")

x1~x5まで、ほぼ同じ範囲に入っており相関の強さが視覚的に確認できました
復習のためにy3を残しておきます
[,1] [,2] [,3] [,4] [,5] [1,] 0.10151443 2.499704243 5.9057675 -3.4943595 -1.3900978 [2,] 1.50663613 5.280020390 6.0871375 -1.6427891 4.1792270 [3,] 5.15807547 9.240978804 10.1524971 1.6396755 4.2384627 [4,] 0.52636740 7.362142992 8.2131410 -2.7272272 -0.1657287 [5,] -1.82768487 2.078275786 4.8978490 -1.3363880 -2.6741024 [6,] 4.43524347 8.060044313 8.8144178 2.4425139 2.0623879 [7,] 0.37328244 5.317456919 3.7818383 -1.0436226 -0.7600355 [8,] -4.91121977 -0.627691232 3.4766397 -4.2966815 -1.9693309 [9,] 3.08701302 4.490715808 8.0062255 1.3102477 3.4494656 [10,] -1.07464046 4.124389139 4.1597881 -3.2331504 -1.5478108 [11,] -4.98187707 -2.960175387 -1.1852294 -8.4042762 -6.7175592 [12,] 0.55455335 4.811030651 4.4954359 -2.1924783 -1.6559525 [13,] -3.25343072 0.216598109 2.5139412 -4.0381462 -2.4717920 [14,] 0.71190379 0.664704194 7.4396890 1.2862593 -0.7421359 [15,] 2.05860252 2.432888164 3.5347403 -1.8087834 -1.5556714 [16,] -4.35657559 0.316841111 1.6688628 -5.3447686 -4.5653558 [17,] 0.52655249 0.326658121 3.3274462 -5.0033717 -1.4797982 [18,] -0.51997740 1.522057422 3.9754390 -2.2568758 -3.4186446 [19,] -2.48896458 0.609983346 4.4815961 -4.4651604 0.5507060 [20,] -1.27166463 0.860673117 4.5316817 -1.6695152 -1.5116476 [21,] 2.36579566 8.115692097 10.1842162 1.5469158 1.2745295 [22,] -2.61885567 2.264994539 1.8073273 -4.6059818 -5.2668700 [23,] -2.87195778 -0.354779514 4.4273497 -2.1824915 -2.3847656 [24,] -0.31689104 4.490830114 7.2127744 0.8737950 3.2108026 [25,] 0.86603870 3.574589801 4.4276743 -1.6189355 -0.6536883 [26,] -1.08641447 1.650209214 0.2495224 -3.6113148 -3.8762204 [27,] -1.06718456 1.333869467 2.7389823 -6.0151694 -1.0285024 [28,] 2.92878284 3.572365454 7.5983883 4.4834977 1.1370509 [29,] 1.25628266 3.077046228 4.4049753 -3.9389680 0.8752170 [30,] -2.25266309 1.031792708 2.0312006 -5.2208742 -1.1417857 [31,] -1.83386252 1.464612026 5.4984764 -2.5442451 -2.5926546 [32,] -3.74237017 0.948552374 1.6345401 -5.3518601 -4.3701054 [33,] 1.57641371 2.949825751 7.6793848 2.8385187 2.5930688 [34,] -1.70707918 4.328429267 4.8674954 -2.3957196 -0.6474211 [35,] -0.68729957 0.186676655 6.3561554 -4.9844379 -2.6635800 [36,] -5.70176744 0.002329385 3.3561491 -3.6218192 -2.5791208 [37,] 0.73014712 2.200125852 3.0212866 -1.4821494 -3.4750934 [38,] 2.51743524 4.256512695 3.2907951 1.0304869 3.3052088 [39,] -3.71975203 -0.761618136 3.5496253 -2.0532424 -1.8430078 [40,] 4.00292393 6.456935876 9.6564018 1.9699281 0.9976009 [41,] -0.76466675 5.343766540 4.4333739 -0.7760534 -1.2543057 [42,] -5.23139631 -2.144231142 0.3253171 -7.3690128 -5.2907999 [43,] 0.22047353 0.598735545 5.6964360 -3.8599177 0.1664410 [44,] 0.25324554 4.186434455 3.3374806 -2.2359334 -2.5759674 [45,] -0.33142225 3.259191383 4.9409355 -4.1641440 -3.3400309 [46,] 4.28859451 7.946808493 9.4197735 1.7908695 1.2385851 [47,] 0.91987986 4.440995369 4.2562333 -4.3308892 -1.1173378 [48,] -3.44169133 0.376280288 2.3650166 -3.1425327 -3.2670228 [49,] 0.07415149 2.969230453 5.1548999 -1.9221235 2.5954580 [50,] 2.51582740 4.186680476 6.5627895 1.7226084 3.3340985
データ取り込みと保存
クリップボードから一覧表の形式に取り込み
エクセルなどの一覧表から必要な部分をコピーします.

その後、いかのような操作でRに取り込むことができます.
#x のなかに一覧表として取り込みます x <- read.table("clipboard",header = T) #xを確認すると ID A B C 1 x1 10.5 8.9 9.9 2 x2 11.2 9.9 10.6 3 x3 9.5 10.2 11.5 4 x4 10.6 8.5 12.3 5 x5 12.3 13.2 11.3 #x2のなかに1列目のIDを行名として取り込む場合 x2 <- read.table("clipboard",header = T, row.names=1) #x2を確認するとIDというラベルが消えて、IDは行名として扱われます A B C x1 10.5 8.9 9.9 x2 11.2 9.9 10.6 x3 9.5 10.2 11.5 x4 10.6 8.5 12.3 x5 12.3 13.2 11.3
列の取り出し
x2のなかのAとBをそれぞれ取り出します
x2$A [1] 10.5 11.2 9.5 10.6 12.3 x2$B [1] 8.9 9.9 10.2 8.5 13.2
取り出したAとBをt検定してみます
t.test(x2$A,x2$B) Welch Two Sample t-test data: x2$A and x2$B t = 0.71918, df = 6.2608, p-value = 0.498 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1.610436 2.970436 sample estimates: mean of x mean of y 10.82 10.14
cvsファイルからの取り込み
あらかじめ作業ディレクトリにファイルを保管しておく必要があります.
y <- read.csv("sample01.csv",row.names=1)
データの保存
取り込んだyの一覧表を、テキストとして作業ディレクトリに保存してみます
write.table(y,file = "data.txt") #dataというテキストファイルが作成されます
ベータ分布

- 作者: 小島寛之
- 出版社/メーカー: ダイヤモンド社
- 発売日: 2015/11/20
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (6件) を見る
この本を参考にベータ分布を勉強します.
ベータ分布:ベータ関数により導かれる分布. ベイズ推定の際に事前分布として利用します.
ベータ関数
期待値
分散
グラフを描いてみます
ベータを1に固定してαのみ大きくすると、1より大きくなると指数関数となります.
curve(dbeta(x,1,1),from = 0,to=1,ylim=c(0,5)) #黒 par(new=T) curve(dbeta(x,2,1),from = 0,to=1,ylim=c(0,5),col=2) #赤 par(new=T) curve(dbeta(x,3,1),from = 0,to=1,ylim=c(0,5),col=3) #緑 par(new=T) curve(dbeta(x,4,1),from = 0,to=1,ylim=c(0,5),col=4) #青

αとβをランダムに
curve(dbeta(x,1,1),from = 0,to=1,ylim=c(0,3)) #黒 par(new=T) curve(dbeta(x,2,2),from = 0,to=1,ylim=c(0,3),col=2) #赤 par(new=T) curve(dbeta(x,3,3),from = 0,to=1,ylim=c(0,3),col=3) #緑 par(new=T) curve(dbeta(x,5,3),from = 0,to=1,ylim=c(0,3),col=4) #青

ベータ分布の使用例1
以下は自作(架空)の問題です.
問)ある疾患の患者群で10中で3人が転倒した場合の、転倒確率をベータ分布によるベイズ統計で推測せよ.
10人中3人なのでといのが直観的な確率になるのですが、ベイズ推定では次のように考えることができます. まず転倒する確率をx、転倒しない確率を1-xとします.転倒する確率(x)+転倒しない確率(1-x)=1.xは連続無限に存在するので、確率密度となります(0≦x≦1).ここで、xの事前分布設定のために、xがどの値でも「同様に確からしい」と仮定します.つまりxの事前分布を下図のような一様分布と仮定します.

「転倒した患者3名、転倒しなかった患者7名」という結果になる確率はとなり、この数式は
のベータ分布です.
したがって転倒確率は となります.
ベータ分布の使用例2
A君は身体に障害をもっており、ただいま装具装着の練習中です.30秒以内で装着できる成功確率をxとして考えてみます.
今日は8回練習して、5回成功しました.A君の装具装着の成功率はどれくらいでしょうか? ベータ分布の使用例1と同じように、xの事前分布設定のために、xがどの値でも「同様に確からしい」と考えて一様分布を仮定します.
確率は となります.現在のA君の装具装着確率は以下のようになります.
curve(dbeta(x,6,4),from = 0,to=1,ylim=c(0,3))

事前分布が同様に確からしいということもありえないので、A君の今日の成功確率を事前分布として確率分布を推定してみます.ここでは正規化定数となるベータ関数を無視して確率分布のみを求めてみます.
P( 現状の成功確率 , 成功確率 ) = P(x) × 事前分布 =
となり以下のような確率分布(赤)となります.
curve(dbeta(x,6,4),from = 0,to=1,ylim=c(0,3)) par(new=T) curve(dbeta(x,7,4),from = 0,to=1,ylim=c(0,3),col=2)

感想)理学療法士が適切な事前分布を設定して、子どもたちの可能性を探るって重要なことだと思いました.
データフレームからの抽出 2
準備
下のデータをコピーして、Rでフレームにします
実験A 10 6 10 9 10 実験B 10 5 5 12 4 実験C 5 4 11 4 6 実験D 9 5 2 3 1
コピーして、データフレームに取り込み
(x <- read.table("clipboard",row.names = 1)) V2 V3 V4 V5 V6 実験A 10 6 10 9 10 実験B 10 5 5 12 4 実験C 5 4 11 4 6 実験D 9 5 2 3 1
列名を記載
cn <- LETTERS[1:5] colnames(x) <- cn x A B C D E 実験A 10 6 10 9 10 実験B 10 5 5 12 4 実験C 5 4 11 4 6 実験D 9 5 2 3 1
データフレームをベクトルに
準備したフレームxから2列目のみを取り出してみます
#列の取り出しは簡単です x[,2] [1] 6 5 4 5
準備したフレームxから2行目のみを取り出してベクトルにします
#2行目 x[2,] A B C D E 実験B 10 5 5 12 4 #2行目をベクトルに変換 (xv <- as.integer(x[2,])) [1] 10 5 5 12 4
マトリックスにしてベクトルとして一括抽出
(xm <- as.matrix(x)) A B C D E 実験A 10 6 10 9 10 実験B 10 5 5 12 4 実験C 5 4 11 4 6 実験D 9 5 2 3 1 (as.vector(xm)) [1] 10 10 5 9 6 5 4 5 10 5 11 2 9 12 4 3 10 4 6 1
因子ベクトル(カテゴリカルデータ)
実験A 10 6 10 9 10 a 実験B 10 5 5 12 4 a 実験C 5 4 11 4 6 b 実験D 9 5 2 3 1 b
コピーしてRのフレームに取り込みます
(xc <- read.table("clipboard",row.names = 1)) V2 V3 V4 V5 V6 V7 実験A 10 6 10 9 10 a 実験B 10 5 5 12 4 a 実験C 5 4 11 4 6 b 実験D 9 5 2 3 1 b cn2 <- LETTERS[1:6] colnames(xc) <- cn2 xc A B C D E F 実験A 10 6 10 9 10 a 実験B 10 5 5 12 4 a 実験C 5 4 11 4 6 b 実験D 9 5 2 3 1 b
上記のような場合には文字が因子に自動的に変換されています
#5列目は整数、6列目は因子 class(xc[,5]) [1] "integer" class(xc[,6]) [1] "factor"
A列、B列のF列bのみ取り出す
subset(xc,select = c(A,B),subset = F=="b") A B 実験C 5 4 実験D 9 5
A列、B列 の F列a VS b
matrixからベクトルに変換してa VS bの配列にします
(xxx <- c(as.vector(as.matrix(xca)),as.vector(as.matrix(xcb)))) xxx [1] 10 10 6 5 5 9 4 5 (dat <- array(xxx, dim = c(2,2,2))) , , 1 [,1] [,2] [1,] 10 6 [2,] 10 5 , , 2 [,1] [,2] [1,] 5 4 [2,] 9 5
項目名などを記入
name <- list("実験"=c("実験A","実験B"),"結果"=c("A","B"),F=c("a","b")) dimnames(dat)<-name dat , , F = a 結果 実験 A B 実験A 10 6 実験B 10 5 , , F = b 結果 実験 A B 実験A 5 4 実験B 9 5
共分散構造分析(パス図の描き方)
Rを使ったパス図作成の方法を忘れないうちに簡単に書いておきます
青木先生のデータを借用しまして勉強していきます.
R -- 因子分析(factanal を援用する)
dat <- matrix(c( -1.89, -0.02, 0.42, 1.23, -1.53, 0.06, 1.81, -0.59, -0.75, -0.12, 2.58, -0.20, -1.92, -0.49, -0.35, 0.69, -0.66, -0.77, -1.92, 0.38, -1.05, 0.07, -0.37, -0.89, -1.62, -2.73, 1.40, 0.18, -0.09, 0.13, 0.95, 0.84, 1.19, 1.19, 0.10, 0.93, 1.17, -1.70, 1.46, -0.25, -0.04, -0.12, -0.34, -0.24, 1.88, 0.16, 1.03, -0.05, -0.73, 0.04 ), byrow=TRUE, ncol=5) colnames(dat) <- c("v1","v2","v3","v4","v5") #列名を加えます x <- dat
相関行列、共分散行列
#後でsemパッケージのために必要になります r <- cor(x) # 相関行列 cov <- cov(x) # 共分散行列
ここはモデルをイメージするところで、色々なパターンが考えられます
RjpWikiに習って、下記のようなイメージで作業を進めて行きます.

library(sem) model <- specifyModel() v1 < F1,path1,1 v2 < F1,path2,NA v3 < F1,path3,NA v4 < F1,path4,NA v5 < F1,path5,NA v1 <> v1,s1,NA v2 <> v2,s2,NA v3 <> v3,s3,NA v4 <> v4,s4,NA v5 <> v5,s5,NA F1 <-> F1,NA,1 #終了したらCtrl+R
いよいよsemパケージを使用します
相関行列を使用したSEM
library(sem) # semパッケージ ans1 <- sem(model, r, N=10) #相関行列を使用してsemを実行 summary(ans1) Model Chisquare = 1.925355 Df = 5 Pr(>Chisq) = 0.8593742 AIC = 21.92536 BIC = -9.58757 Normalized Residuals Min. 1st Qu. Median Mean 3rd Qu. Max. -0.3976000 -0.0000002 0.0155300 0.1221000 0.2435000 0.6971000 R-square for Endogenous Variables v1 v2 v3 v4 v5 0.6297 0.0809 0.4573 0.0583 0.0506 Parameter Estimates Estimate Std Error z value Pr(>|z|) path1 0.7935558 0.4882341 1.6253592 0.10408604 v1 <--- F1 path2 -0.2843858 0.3849962 -0.7386717 0.46010637 v2 <--- F1 path3 -0.6762525 0.4525192 -1.4944171 0.13506663 v3 <--- F1 path4 -0.2414672 0.3860898 -0.6254172 0.53169727 v4 <--- F1 path5 0.2248359 0.3864879 0.5817413 0.56074096 v5 <--- F1 s1 0.3702693 0.6626860 0.5587401 0.57633909 v1 <--> v1 s2 0.9191248 0.4485423 2.0491376 0.04044867 v2 <--> v2 s3 0.5426826 0.5322169 1.0196644 0.30788765 v3 <--> v3 s4 0.9416935 0.4546109 2.0714275 0.03831887 v4 <--> v4 s5 0.9494489 0.4567576 2.0786712 0.03764758 v5 <--> v5 Iterations = 15 #Estimate の部分が非標準化係数ですが、相関行列から求めているので不正確
標準化係数
stdCoef(ans1) # 標準化係数 Std. Estimate path1 path1 0.7935557 v1 <--- F1 path2 path2 -0.2843858 v2 <--- F1 path3 path3 -0.6762525 v3 <--- F1 path4 path4 -0.2414672 v4 <--- F1 path5 path5 0.2248359 v5 <--- F1 s1 s1 0.3702693 v1 <--> v1 s2 s2 0.9191247 v2 <--> v2 s3 s3 0.5426826 v3 <--> v3 s4 s4 0.9416936 v4 <--> v4 s5 s5 0.9494488 v5 <--> v5 1.0000000 F1 <--> F1
共分散行列を使用したSEM
ans2 <- sem(model, cov, N=284) # 非標準化係数 summary(ans2) Model Chisquare = 60.54173 Df = 5 Pr(>Chisq) = 9.392241e-12 AIC = 80.54173 BIC = 32.29686 Normalized Residuals Min. 1st Qu. Median Mean 3rd Qu. Max. -2.230000 -0.000001 0.087080 0.684600 1.365000 3.909000 R-square for Endogenous Variables v1 v2 v3 v4 v5 0.6297 0.0809 0.4573 0.0583 0.0506 Parameter Estimates Estimate Std Error z value Pr(>|z|) path1 1.2135217 0.13314543 9.114257 7.921129e-20 v1 <--- F1 path2 -0.2329064 0.05622870 -4.142127 3.440994e-05 v2 <--- F1 path3 -0.6310501 0.07530436 -8.379995 5.293016e-17 v3 <--- F1 path4 -0.2643794 0.07538517 -3.507048 4.531080e-04 v4 <--- F1 path5 0.2209609 0.06773505 3.262135 1.105764e-03 v5 <--- F1 s1 0.8658805 0.27636060 3.133155 1.729383e-03 v1 <--> v1 s2 0.6164834 0.05365106 11.490610 1.470704e-30 v2 <--> v2 s3 0.4725590 0.08264694 5.717805 1.079092e-08 v3 <--> v3 s4 1.1288825 0.09718675 11.615601 3.433641e-31 v4 <--> v4 s5 0.9170030 0.07867069 11.656221 2.133019e-31 v5 <--> v5 #Estimate ここは間違いなく非標準化係数です
パス図の作成
install.packages("DiagrammeR") install.packages("scales") pathDiagram(ans1, ignore.double=FALSE, edge.labels="values", digits=3, node.font=c("HGRGE", 10)) pathDiagram(ans2, ignore.double=FALSE, edge.labels="values", digits=3, node.font=c("HGRGE", 10))


lavaanパッケージによる方法
RjpWikiより
installed.packages("lavaan") library("lavaan") model2 <- 'f1 =~ v1 + v2 + v3 + v4 + v5 ' ans3 <- cfa(model=model2, data=x, std.lv=TRUE, mimic="EQS") # mimicオプションを"EQS"とするとsemパッケージの結果と一致する。デフォルトでは"Mplus" summary(ans3, fit.measures=TRUE, standardize = TRUE) standardizedSolution(object =ans3 )# 標準化推定値 lhs op rhs est.std se z pvalue 1 f1 =~ v1 -0.794 NA NA NA 2 f1 =~ v2 0.284 NA NA NA 3 f1 =~ v3 0.676 NA NA NA 4 f1 =~ v4 0.241 NA NA NA 5 f1 =~ v5 -0.225 NA NA NA 6 f1 ~ f1 -3.576 NA NA NA 7 v1 ~~ v1 0.370 NA NA NA 8 v2 ~~ v2 0.919 NA NA NA 9 v3 ~~ v3 0.543 NA NA NA 10 v4 ~~ v4 0.942 NA NA NA 11 v5 ~~ v5 0.949 NA NA NA 12 f1 ~~ f1 1.000 NA NA NA
信頼区間のプロット
同じサイズのデータサンプルからt分布を利用した信頼区間の作図
まずは3×4の場合(サンプルサイズ3を4回実施する)
x <- matrix(NA,nrow=3,ncol=4) #3×4の空セル for (i in 1:4){ #列数分乱数を代入 x[,i] <- rnorm(3) #標準正規分布の乱数を行数分繰り返す } mx <- rowMeans(x) #行平均を一括計算 mean(x[1,]) #1行目のみ取り出して確認 vx <- apply(x,1,var) #行分散を一括計算 var(x[1,]) #1行目のみ取り出して確認 lx1 <- mx+qt(0.975,2)*sqrt(vx/3) #95%信頼区間の上限(平均+t値*標準誤差), lower.tail=TRUE lx2 <- mx-qt(0.975,2)*sqrt(vx/3) #95%信頼区間の下限(平均-t値*標準誤差), (0.975,2, lower.tail=F )=qt(0.025,2,lower.tail=FALSE ) par(mfrow = c(1,2)) #1行2列に図を並べます plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="") plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="") dev.off() #作図を終了します #t値はqt(0.025,2)~qt(0.975,2)になります, lower.tail=TRUE
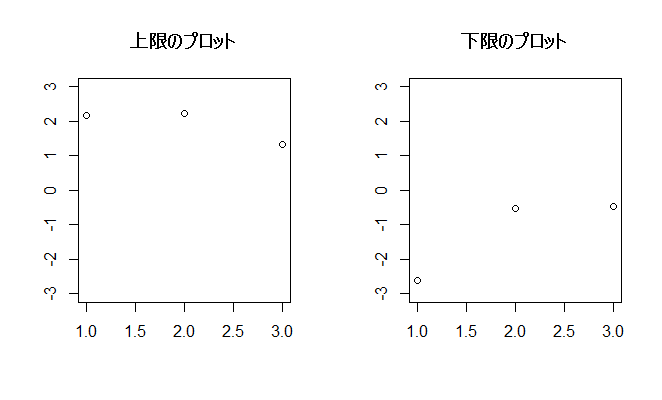
行列数値を増やしていけば見えてきます 1000行10列でやってみます
x <- matrix(NA,nrow=1000,ncol=10) for (i in 1:10){ x[,i] <- rnorm(1000) } mx <- rowMeans(x) vx <- apply(x,1,var) lx1 <- mx+qt(0.975,9)*sqrt(vx/10) lx2 <- mx-qt(0.975,9)*sqrt(vx/10) par(mfrow = c(1,2)) plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="") plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="") dev.off()
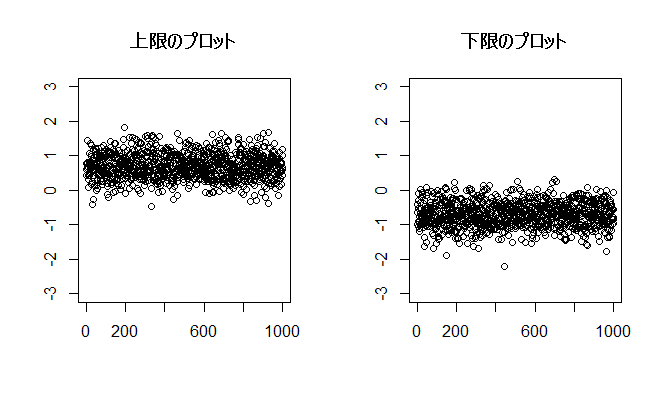
行数=r,列数=lとした場合
x <- matrix(NA,nrow=r,ncol=l) for (i in 1:l){ x[,i] <- rnorm(r) } mx <- rowMeans(x) vx <- apply(x,1,var) lx1 <- mx+qt(0.975,l-1)*sqrt(vx/l) lx2 <- mx-qt(0.975,l-1)*sqrt(vx/l) par(mfrow = c(1,2)) plot(lx1, ylim = c(-3,3), main = "上限のプロット", ylab="", xlab="") plot(lx2, ylim = c(-3,3), main = "下限のプロット", ylab="", xlab="") dev.off()