対応のないt検定の検定力分析(事後の分析)
検定力(1-β):帰無仮説が「偽」であるとき(母集団に差があるとき)にサンプルから有意差を得る確率
効果量(effect size):標準化された平均値差(検定により色々あります...d family, r family)
標本数:研究者が決定しなければならない
α(有意水準):慣例的に5%、1%で固定されている
検定力分析を実行する場合に、効果量の問題を解決しなければなりません.効果量を表す指標は数多く存在するので、まずどれを使うかが問題となります.今回はt検定の検定力分析に利用されている、次の二つの効果量について勉強していきます.
効果量=効果の大きさ
実験的操作の効果、変数間の関係性の強さを表す指標(大 中 小)
Cohoen's d : グループごとの平均値の差を標準化したd family
r : 変数間の関係の強さを示すr family
効果量の目安
小 中 大
d 0.2 0.5 0.8
r 0.1 0.3 0.5
まずは記号の定義・・・これ大事
母平均μx, 標本x, サイズm, 標本平均xa, 不偏分散
母平均μy, 標本y, サイズn, 標本平均ya, 不偏分散
標本効果量(cohensのd効果量)の求め方
d = xの平均値とyの平均値の差の絶対値÷2群の共通の標準偏差
プールした分散
例 x <- c(39, 47, 48, 59, 65, 68, 74, 79, 80, 82, 87, 88, 89, 94, 99) y <- c(25, 27, 32, 37, 38, 44, 45, 52, 54, 60, 65, 67, 68, 69, 71) pool <- ((length(x) - 1) * var(x) + (length(y) - 1) * var(y)) / (length(x) + length(y) - 2) t <- (mean(x) - mean(y)) / sqrt((pool / length(x)) + (pool / length(y))) = 3.6449 d <- (abs(mean(x) - mean(y)))/pool =1.33 (dは1を超える場合もある)
Rを使ってt値から算出してみます
t.test(x,t,var.equal = T) d = t*sqrt((length(x)+length(y))/length(x)*length(y)) = 3.6449*sqrt(30/(15*15)) = 1.33
Rを使って検定力を算出します
library(pwr) pwr.t2n.test(n1=15,n2=15, d =1.33 , sig.level =0.05 , power = NULL,alternative = "greater")
t test power calculation
n1 = 15
n2 = 15
d = 1.33
sig.level = 0.05
power = 0.971769
alternative = greater
power = 0.97より、帰無仮説が偽の場合に有意差が検出される確率は97%です.高い検定力であると言えます.
標本効果量(r)の求め方
t.test(x,y,var.equal = T) t = 3.6449 r <- sqrt(t^2/(t^2+18)) =0.6516516
効果量は「大」でした
参考)水本篤; 竹内理. 研究論文における効果量の報告のために―基本的概念と注意点―. 2008.
2標本 平均の差の検定
下記のサイトに移転しました
確率点と累積分布
確率点と累積分布
投稿日2017.7.22
更新日2017.9.1
lower.tailのdefaultはTRUE
この意味が重要です.勉強のためにdefaultのTRUEも挿入しときます.
lower.tail
logical; if TRUE (default), probabilities are P[X ≤ x] otherwise, P[X > x].
Rのhelpより
#上側確率が0.025になるZ値 qnorm(0.975, lower.tail = TRUE) = 1.959964 # Z=1.959964 より下側の累積確率が0.975 ) qnorm(0.975, lower.tail = FALSE) = -1.959964 # Z= -1.959964 より上側の累積確率が0.975 ) #上側確率が0.025になる累積分布 pnorm(1.96, lower.tail = TRUE) = 0.9750021 #下側確率が0.025になる累積分布 pnorm(1.96, lower.tail = FALSE) = 0.0249979
二項分布
イメージするためにグラフ挿入 x <- 0:3 y <- c(dbinom(x, 3, 0.5)) names(y) <- x barplot(y)

#試行回数n, 成功回数x, 確率pの場合の累積確率は dbinom(n, x, p) #確率0.5のベルヌーイ試行(成功,失敗)で3回実施して成功が2回以内の確率は pbinom(2, 3, 0.5, lower.tail = TRUE) = 0.875 #確率0.5のベルヌーイ試行(成功,失敗)で3回実施して成功が2回以上の確率は pbinom(2, 3, 0.5, lower.tail = FALSE) = 0.125
t分布
#自由度10、上側確率が0.025になるt値 qt(0.975, 10, lower.tail = TRUE) = 2.228139 #下側確率が0.025になるt値 qt(0.025, 10, lower.tail = TRUE) = qt(0.975, 10, lower.tail = FALSE) = -2.228139
F分布
#自由度(6, 24), 確率0.05のF値 qf(0.95, 6, 24, lower.tail = TRUE) = 2.508189 #自由度(6, 24), F値がfの場合の累積確率 pf(f, 6, 24, lower.tail = TRUE) = 0.95 #その場合のp値 pf(f, 6, 24, lower.tail = FALSE) = 1 - pf(f, 6, 24) = 0.05
ブログの再構成
自分が書いたブログなのに「見にくい&理解できない」 という悩みが募ってきました. よって、少しずつ再構成することにしました. はてな記法なるものに初挑戦! 見直したとき、せめて・・・ せめて書いた本人が理解できるような内容に改めたいと思っております.
モンティ・ホール問題
モンティ・ホール問題
投稿日2017.8.30
モンティ・ホール問題、モンティ・ホール・ジレンマ
Rを使って何とか解いてみようと思います.
3つのドアのうち1つのドアの後ろには高級車(車の扉)があり、残りの2つのドアにはヤギ(ヤギの扉)がいます。司会者は、どのドアの後ろに高級車があるのかを知っています。
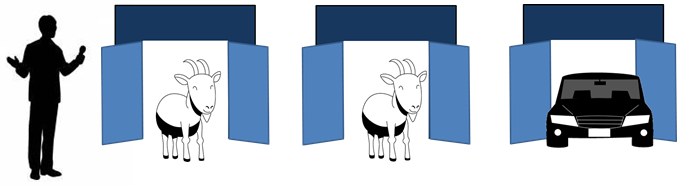
あなたが1つのドアを選んだ(最初の扉)あと、司会者はあなたが選んでいない2つのドアの1つのドアを開けてヤギがいることを教えてくれます。
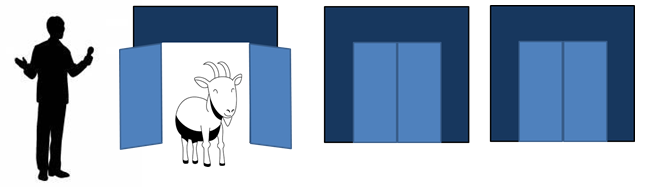
そして司会者は・・・
「はじめに選んだドア(最初の扉)のままでもよいし、いま閉じられているドアを選択してもよい」と言ってきました。司会者はウソはつきません。あなたははじめに選択したドアのままにしますか?それともドアを変更しますか?
出典:稲葉由之 ;プレステップ統計学II 推測統計学,弘文堂,2013,p30
残り二つの扉、どちらを選択しても確率は1/2のように思えるのですが・・・
嘘みたいですけど、このことが長年大論争になったそうです.今回は、Rを使って確率の勉強をしてみたいと思います.

このように考えると、扉を変更した方が2/3になりそうだけど・・・1/2じゃない
10回、100回、1000回・・・やったらどうなるかいな?
ということでRを使ってシミュレーションを実行してみます
まず扉のNoを1,2,3とします

扉には doors <- c(1:3) という名前をつけます.
車の扉、最初の扉、ヤギの扉をランダムに割り当ててみます.
もちろん車の扉=最初の扉の場合もありますので、「車の扉」と「最初の扉」の抽出は復元抽出になります.
sampleを使用してランダム抽出します
car <- sample(doors, 1) you <- sample(doors, 1)
扉を変えない場合
notcha <- function(x){ doors <- c(1:3) x <- 0 car <- sample(doors, 1) #ランダム抽出で車の扉を設定 you <- sample(doors, 1) #ランダム抽出で最初の扉を設定 if(car == you){ #もし最初の扉に車の扉だったら1点加える x <- x + 1 } return(x) } notcha() y <- 0 for(i in 1:10000) { # fro(i in 1:n){} ・・・{}をn回繰り返す y <- y + notcha() } y
10000回実施したら3302回でした.約1/3です.
扉を変えた場合
chan <- function(x){ x <- 0 doors <- c(1:3) car <- sample(doors, 1) #ランダム抽出で車の扉を設定 you <- sample(doors, 1) #ランダム抽出で最初の扉を設定 if(you == car){ x <- x + 0 #最初に選んだ扉に車がある場合、0点となります }else{ x <- x + 1 #最初の扉に車がない場合、残るヤギの扉は司会者が明けているので、必ず車の扉を選択することになります } return(x) } chan() y <- 0 for(i in 1:10000) { # fro(i in 1:n) {} ・・・{}をn回繰り返す y <- y + chan() } y
10000回実施した確率は6656回でした.約2/3です.
こんな解き方では異論が多いと思いますので、スマートな方法をネットで検索してみてください
