グラフに色をつける
library(RColorBrewer)
#RColorBrewerパッケージのサンプル
display.brewer.all()
ヒストグラムを塗ってみる
どの色セットを使用するかを指定する
cols <- brewer.pal(8,"Pastel1") # brewer.pal(何色、パレット名)
y<-c(1,2,3,4,5,6,7)
p<-c(2,3,4,5,4,3,2)
q<-c(2,3,4,5,4,3,2)
par(mfrow = c(3,3),mar = c(5, 4, 1, 4)) #余白 底辺、左、上、右の順
pos.x <- barplot(q,ylim=c(0,6),col=cols[1])
pos.x <- barplot(q,ylim=c(0,6),col=cols[2])
pos.x <- barplot(q,ylim=c(0,6),col=cols[3])
pos.x <- barplot(q,ylim=c(0,6),col=cols[4])
pos.x <- barplot(q,ylim=c(0,6),col=cols[5])
pos.x <- barplot(q,ylim=c(0,6),col=cols[6])
pos.x <- barplot(q,ylim=c(0,6),col=cols[7])
pos.x <- barplot(q,ylim=c(0,6),col=cols[8])
pos.x <- barplot(q,ylim=c(0,6),col=cols[9])

棒グラフの中央に散布図をプロットする方法 (pos.x)
y<-c(1,2,3,4,5,6,7)
p<-c(2,3,4,5,4,3,2)
q<-c(2,3,4,5,4,3,2)
par(mar = c(5, 4, 1, 4)) #余白 底辺、左、上、右の順
pos.x <- barplot(q,ylim=c(0,6))
points(pos.x, p)

Rで簡単(t検定の検定力分析)
パッケージpwrを使用します
library(pwr)
pwr.t.test(n = , d = , sig.level = , power = , type = c("two.sample", "one.sample", "paired"))
n=標本数
d=効果量()
sig.level=有意水準
power=検定力
type=t検定の形("two.sample=対応なし", "one.sample=1標本", "paired=対応あり")
n, d, power, and sig.level のいずれかを空白(NULL)にします
strict=T #厳密な検定が可能になる
(効果量(effect size)のはなし - 六本木で働くデータサイエンティストのブログ)
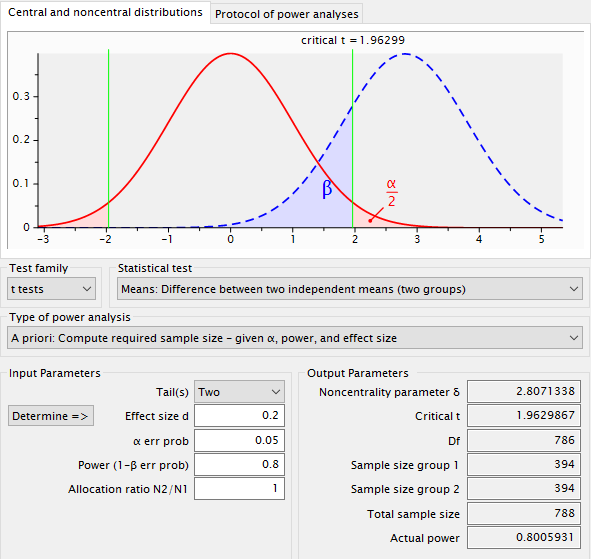
必要な標本数を求めてみます
pwr.t.test(n =NULL, d =0.2 , sig.level =0.05 , power = 0.8, type ="two.sample")
Two-sample t test power calculation
n = 393.4057
d = 0.2
sig.level = 0.05
power = 0.8
alternative = two.sided
効果量0.2、有意水準0.05、検定力0.8の場合の標本の大きさは393必要になります
もちろんフリーソフトG*powerを使用した結果と同じになります
効果量をもとめてみます
pwr.t.test(n =150, d =NULL , sig.level =0.05 , power = 0.8, type ="two.sample")
Two-sample t test power calculation
n = 150
d = 0.3245459
sig.level = 0.05
power = 0.8
alternative = two.sided
標本数150、有意水準0.05、検定力0.8の場合の効果量は0.32と低くなります
フリーソフトG*powerを使用した結果

Rの予備知識
for(i in c(2,4,6)) でiに2,4,6を順に挿入する命令
print(・・・) 引数が数値ベクトルの場合にはベクトルの中身を表示する
print(c(1,2,3))
合わせて
for(i in c(0.26,0.24,0.22)){print(x<-c(i+1))}
round 四捨五入を導入して・・・
for(i in c(0.26,0.24,0.22)){print(round(x<-c(i+1),1))}
上記を利用して
有意水準が.05,.01,.001)のときの対応なしt検定のpowerを一気に算出してみます
pwr.t.test(n =NULL,d =0.2,sig.level=0.05,power=0.8,type ="two.sample")
for(i in c(.05,.01,.001)){print(round(pwr.t.test(n =394,d =0.2,sig.level=i,
,type ="two.sample")$power,2))}
[1] 0.8
[1] 0.59
[1] 0.31
対応のなし(2群の標本数が異なる場合)
pwr.t2n.test(n1 = , n2= , d = , sig.level =, power = )
例)
pwr.t2n.test(n1 =120, n2=NULL , d =0.5 , sig.level =0.05, power =0.8 )
t test power calculation
n1 = 120
n2 = 43.21666
d = 0.5
sig.level = 0.05
power = 0.8
alternative = two.sided
n1=120、効果量0.5、有意水準0.05、検定力0.8、両側検定の場合n1=43.2必要
時系列データの可視化01
下のデータをコピーして時系列グラフを作ってみます
心拍変動を三次元加速度を同時測定した結果です
被験者は私です
RRI TEM X Y Z HF LFHF LF activity HR
793 21.5 0.16 -1.09 -0.12 75.531 4.247 80.941 0.11 76
800 21.5 0.16 -1.09 -0.12 75.436 4.078 80.308 0.11 75
785 21.5 -0.19 -1.06 -0.28 76.456 4.069 80.271 0.11 76
800 21.5 -0.19 -1.06 -0.28 75.99 4.136 80.529 0.11 75
771 21.5 -0.19 -1.06 -0.28 79.091 3.808 79.203 0.11 78
777 21.5 -0.19 -1.06 -0.28 80.769 3.654 78.515 0.11 77
786 21.5 -0.19 -1.06 -0.28 82.759 3.52 77.876 0.11 76
778 23.1 0.19 -1.09 -0.19 84.894 3.408 77.316 0.13 77
790 23.1 0.19 -1.09 -0.19 87.254 3.308 76.789 0.13 76
784 23.1 0.19 -1.09 -0.19 89.791 3.215 76.277 0.13 77
718 23.1 0.19 -1.09 -0.19 92.463 3.123 75.746 0.13 84
721 23.1 0.19 -1.09 -0.19 95.281 3.025 75.156 0.13 83
698 23.1 0.12 -1 -0.62 98.16 2.92 74.493 0.19 86
717 23.1 0.12 -1 -0.62 101.123 2.82 73.824 0.19 84
728 23.1 0.12 -1 -0.62 103.987 2.724 73.15 0.19 82
782 23.1 0.12 -1 -0.62 107.143 2.637 72.503 0.19 77
711 23.1 0.12 -1 -0.62 110.228 2.544 71.781 0.19 84
705 23.1 0.12 -1 -0.62 109.643 2.538 71.738 0.19 85
710 23.1 -0.31 -1.16 -0.56 112.757 2.448 71.001 0.32 85
697 23.1 -0.31 -1.16 -0.56 116.133 2.363 70.267 0.32 86
697 23.1 -0.31 -1.16 -0.56 119.019 2.283 69.545 0.32 86
682 23.1 -0.31 -1.16 -0.56 122.16 2.206 68.812 0.32 88
679 23.1 -0.31 -1.16 -0.56 125.184 2.137 68.122 0.32 88
Rに貼り付けます
x<-read.table("clipboard",header=T)
TEM<-ts(x$TEM)
HR<-ts(x$HR)
RRI<-ts(x$RRI)
LFHF<-ts(x$LFHF)
X<-ts(x$X)
Y<-ts(x$Y)
Z<-ts(x$Z)
activity<-ts(x$activity)
4行2列のベースを用意
par(mfrow=c(4,2))
そこにグラフをプロット
ts.plot(TEM,type="l",main="TEM")
ts.plot(HR,type="l",main="HR")
ts.plot(RRI,type="l",main="RRI")
ts.plot(LFHF,type="l",main="LFHF")
ts.plot(X,type="l",main="X")
ts.plot(Y,type="l",main="Y")
ts.plot(Z,type="l",main="Z")
ts.plot(activity,type="l",main="activity")

いったんグラフを消去します
graphics.off()
次に、グラフィックスパラメータ値を一時退避する方法
par(no.readonly = TRUE) を使って
ts.plot(HR,type="l",main="HR")のみを緑色&破線にしてみます
par(mfrow=c(4,2))
ts.plot(TEM,type="l",main="TEM")
# 現グラフィックスパラメータ値を退避
oldpar <- par(no.readonly = TRUE)
# 一部だけ追加
oldpar <- par(col=3, lty=2)
# 緑色にしたいグラフをプロット
ts.plot(HR,type="l",main="HR")
# 元のグラフィックスパラメータ値に
par(oldpar)
# 残りのグラフをプロット
ts.plot(RRI,type="l",main="RRI")
ts.plot(LFHF,type="l",main="LFHF")
ts.plot(X,type="l",main="X")
ts.plot(Y,type="l",main="Y")
ts.plot(Z,type="l",main="Z")
ts.plot(activity,type="l",main="activity")

参考)田中 孝文; Rによる時系列分析入門, シーエーピー出版, 2008